NCERT Solutions for Class 7 Maths Chapter 10 Practical Geometry| PDF Download
Chapter 10 Practical Geometry NCERT Solutions for Class 7 Maths is available on this page which will help you in fetching good marks in the exams. These NCERT Solutions are prepared by subject matter experts of Studyrankers who have great experience of teaching students. Also, you can download PDF of Chapter 10 Practical Geometry Class 7 Maths NCERT Solutions from this page that can help you in scoring good marks in the exams.
Class 7 Maths textbook will provide you opportunities to learn new things in more exciting way and help in solving the difficulties that lie ahead with ease. It can be used to enrich knowledge and deeper understanding of various topics.

Exercise 10.1
1. Draw a line, say AB, take a point C outside it. Through C, draw a line parallel to AB using ruler and compasses only.
Answer
To construct: A line, parallel to given line by using ruler and compasses.
Steps of construction:
(a) Draw a line-segment AB and take a point C outside AB.
(b) Take any point D on AB and join C to D.
(c) With D as centre and take convenient radius, draw an arc cutting AB at E and CD at F.
(d) With C as centre and same radius as in step 3, draw an arc GH cutting CD at I.
(e) With the same arc EF, draw the equal arc cutting GH at J.
(f) Join JC to draw a line l. This the required line.

2. Draw a line l. Draw a perpendicular to l at any point on l. On this perpendicular choose a point X, 4 cm away from l. Through X, draw a line m parallel to l.
Answer
To construct: A line parallel to given line when perpendicular line is also given.
Steps of construction:
(a) Draw a line l and take a point P on it.
(b) At point P, draw a perpendicular line n.
(c) Take PX = 4 cm on line n.
(d) At point X, again draw a perpendicular line m.
Given figure is the required construction.

3. Let l be a line and P be a point not on l. Through P, draw a line m parallel to l. Now join P to any point Q on l. Choose any other point R on m. Through R, draw a line parallel to PQ. Let this meet l at S. What shape do the two sets of parallel lines enclose?
Answer
To construct: A pair of parallel lines intersecting other part of parallel lines.
Steps of construction:
(a) Draw a line l and take a point P outside of l .
(b) Take point Q on line l and join PQ.
(c) Make equal angle at point P such that ∠Q = ∠P.
(d) Extend line at P to get line m.
(e) Similarly, take a point R online m, at point R, draw angles such that ∠P = ∠R.
(f) Extended line at R which intersects at S online l. Draw line RS.
Thus, we get parallelogram PQRS.

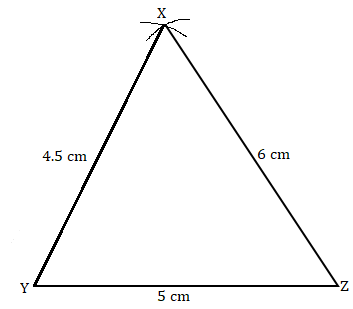
1. Construct ΔXYZ in which XY = 4.5 cm, YZ = 5 cm and ZX = 6 cm.
Answer
To construct: ΔXYZ, where XY = 4.5 cm, YZ = 5 cm and ZX = 6 cm.
Steps of construction:
(a) Draw a line segment YZ = 5 cm.
(b) Taking Z as centre and radius 6 cm, draw an arc.
(c) Similarly, taking Y as centre and radius 4.5 cm, draw another arc which intersects first arc at point X.
(d) Join XY and XZ. It is the required ΔXYZ.
2. Construct an equilateral triangle of side 5.5 cm.
Answer
To construct: A ΔABC where AB = BC = CA = 5.5 cm
Steps of construction:
(a) Draw a line segment BC = 5.5 cm
(b) Taking points B and C as centers and radius 5.5 cm, draw arcs which intersect at point A.
(c) Join AB and AC. It is the required ΔABC.

3. Draw ΔPQR with PQ = 4 cm, QR = 3.5 cm and PR = 4 cm. What type of triangle is this?
Answer
To construction: ΔPQR, in which PQ = 4 cm, QR = 3.5 cm and PR = 4 cm.
Steps of construction:
(a) Draw a line segment QR = 3.5 cm.
(b) Taking Q as centre and radius 4 cm, draw an arc.
(c) Similarly, taking R as centre and radius 4 cm, draw an another arc which intersects first arc at P.
(d) Join PQ and PR. It is the required isosceles ΔPQR.

Answer
To construct: ΔABC in which AB = 2.5 cm, BC = 6 cm and AC = 6.5 cm.
Steps of construction:
(a) Draw a line segment BC = 6 cm.
(b) Taking B as centre and radius 2.5 cm, draw an arc.
(c) Similarly, taking C as centre and radius 6.5 cm, draw another arc which intersects first arc at point A.
(d) Join AB and AC.
(e) Measure angle B with the help of protractor. It is the required ΔABC where ∠B = 80°.

Exercise 10.3
1. Construct ΔDEF such that DE = 5 cm, DF = 3 cm and ∠EDF = 90°.
Answer
To construct: ΔDEF where DE = 5 cm, DF = 3 cm and m ∠EDF = 90°.
Steps of construction:
(a) Draw a line segment DF = 3 cm.
(b) At point D, draw an angle of 90o with the help of compass i.e., ∠XDF = 90°.
(c) Taking D as centre, draw an arc of radius 5 cm, which cuts DX at the point E.
(d) Join EF. It is the required right angled triangle DEF.

2. Construct an isosceles triangle in which the lengths of each of its equal sides is 6.5 cm and the angle between them is 110°.
Answer
To construct: An isosceles triangle PQR where PQ = RQ = 6.5 cm and ∠Q = 110°
Steps of construction:
(a) Draw a line segment QR = 6.5 cm.
(b) At point Q, draw an angle of 110° with the help of protractor, i.e., ∠YQR = 110°
(c) Taking Q as centre, draw an arc with radius 6.5 cm, which cuts QY at point P.
(d) Join PR
Given figure is the required isosceles triangle PQR.

3. Construct ΔABC with BC = 7.5 cm, AC = 5 cm and m ∠C = 60° .
Answer
To construct: ΔABC where BC = 7.5 cm, AC = 5 cm and m ∠C = 60°.
Steps of construction:
(a) Draw a line segment BC = 7.5 cm.
(b) At point C, draw an angle of 60 with the help of protractor, i.e., ∠XCB = 60° .
(c) Taking C as centre and radius 5 cm, draw an arc, which cuts XC at the point A.
(d) Join AB It is the required triangle ABC.

Exercise 10.4
1. Construct ΔABC, given m∠A = 60°, m∠B = 30° and AB = 5,8 cm.
Answer
To construct: ΔABC, given m∠A = 60°, m∠B = 30° and AB = 5,8 cm.
Steps of construction:
(a) Draw a line segment AB = 5.8 cm.
(b) At point A, draw an angle Z YAB = 60°= with the help of a compass.
(c) At point B, draw Z XBA = 30° with the help of a compass.
(d) AY and BX intersect at the point C.
Given figure is the required triangle ABC.

2. Construct Δ PQR if PQ = 5 cm, m∠PQR = 105° and m∠.QRP = 40°.
Answer
Given:
m∠ PQR = 105° and m∠ QRP = 40°
We know that sum of angles of a triangle is 180°.
∴ m∠PQR + m∠QRP + m∠ QPR = 180°
⇒ 105° + 40° + m∠QPR= 180°
⇒ 145° + m∠QPR= 180°
⇒ m∠QPR= 180° - 145°
⇒ m∠QPR = 35°
To construct: ΔPQR where m∠P = 35°, m∠Q = 105° and PQ = 5 cm.
Steps of construction:
(a) Draw a line segment PQ = 5 cm,
(b) At point P, draw ∠ XPQ = 35° with the help of protractor.
(c) At point Q, draw ∠ YQP = 105° with the help of protractor.
(d) XP and YQ intersect at point R.
It is the required triangle PQR.

3. Examine whether you can construct ΔDEF such that EF = 7.2 cm, m∠ E= 110° and m∠F= 80°. Justify your answer.
Answer
Given: In ΔDEF, m∠E = 110° and m∠T = 80°
Using angle sum property of triangle
∠D + ∠E + ∠F = 180°
⇒∠D + 110°+ 80° = 180°
⇒ ∠D + 190° = 180°
⇒ ∠D = 180° - 190° = -10°
Which is not possible.
Exercise 10.5
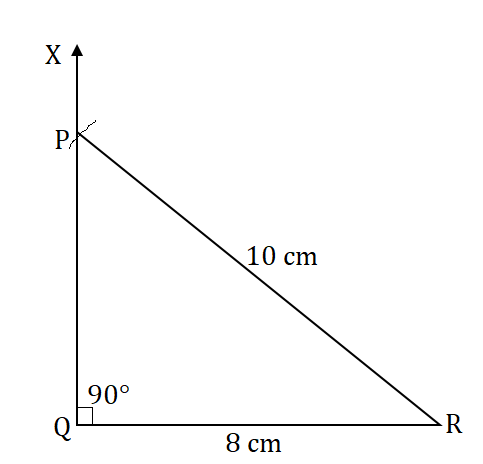
1. A right angled triangle PQR where m∠Q = 9ff, QR= 8 cm and PQ = 10 cm.
Answer
To construct: Construct the right angled Δ PQR, where m∠Q = 90", QR = 8 cm and PR = 10 cm.
Steps of construction:
(a) Draw a line segment QR = 8 cm,
(b) At point Q, draw QX ⊥ QR,
(c) Taking R as centre, draw an arc of radius 10 cm.
(d) This arc cuts QX at point P.
(e) foin PQ.
Given figure is the required right-angled triangle PQR,
2. Construct a right-angled triangle whose hypotenuse is 6 cm long and one the legs is 4 cm long.
Answer
To construct: A right-angled triangle DEF where DF = 6 cm and EF = 4 cm.
Steps of construction:
(a) Draw a line segment EF = 4 cm.
(b) At point Q, draw EX ⊥ EF.
(c) Taking F as centre and radius 6 cm, draw an arc. (Hypotenuse)
(d) This arc cuts the EX at point D.
(e) Join DF.
It is the required right-angled triangle DEF.

3. Construct an isosceles right angled triangle ABC, where m∠ACB = 90° and AC = 6 cm.
Answer
To construct: An isosceles right angled triangle ABC where m∠ C = 90% AC = BC = 6 cm.
Steps of construction:
(a) Draw a line segment AC = 6 cm.
(b) At point C, draw XC ⊥ CA.
(c) Taking C as centre and radius 6 cm, draw an arc.
(d) This arc cuts CX at point B.
(e) Join BA.
It is the required isosceles right-angled triangle ABC.

Go Back To NCERT Solutions for Class 7 Maths
NCERT Solutions for Class 7 Maths Chapter 10 Practical Geometry
Chapter 10 NCERT Solutions are prepared as per the accordance of latest CBSE guidelines so you can score maximum marks. In this chapter, we will will learn how to draw parallel lines and some types of triangles.
• To construct a triangle, we should know any one of the following:
(i) Length of the three sides
(ii) Two sides and the included angle
(iii) Two angles and the included side
(iv) Length of the hypotenuse and one side in case of a right-angled triangle.
• Properties of angles formed by parallel lines and transversal:
(i) All pairs of alternate interior angles formed by parallel lines and a transversal are equal.
(ii) All pairs of corresponding angles formed by parallel lines and a transversal are equal.
(iii) All pairs of alternate exterior angles formed by parallel lines and a transversal are equal.
(iv) The interior angles formed on the same side of the transversal are supplementary (the sum of their measures is 180°).
You can find exercisewise Class 7 NCERT Solutions by clicking on the links given below. These NCERT Solutions are necessary guide to frame good answers in the examinations.
NCERT Solutions will improve your retention memory and studying habits. It will help a student in analyzing the problems and answering it with precision and the right concepts. Students can develop their understanding of the chapter and obtain maximum marks in the exams.
NCERT Solutions for Class 7 Maths Chapters:
FAQ on Chapter 10 Practical Geometry
How many exercises are there in Chapter 10 Practical Geometry Class 7 Maths NCERT Solutions?
There are five exercises in the Chapter 10 NCERT Solutions which will help in learning how to solve a questions efficiently. A student will gain confidence that is going to help them in exams by solving these Class 7 Maths NCERT Solutions.
__________ line (s) can be drawn parallel to a given line.
Infinite line (s) can be drawn parallel to a given line.
How many lines can be drawn parallal to a given line, through a point outside the given line?
One line can be drawn parallal to a given line, through a point outside the given line.
Which geometrical instrument can be used to draw an arc?
Compass is used to draw an arc.

