Download App

Chapter 1 Real Numbers Important Questions for CBSE Class 10 Maths Board Exams

This page contains Important Questions for Class 10 Maths Chapter 1 Real Numbers, which will help the students to prepare for the CBSE Class 10 maths Board exam 2022-23. It help the doing better in their maths paper. Extra questions of Chapter 1 Real Numbers given here which are based on the pattern of CBSE NCERT book. Students will learn about the entire syllabus and learn how to solve problems in preparation for the exams.

Important Questions for Chapter 1 Real Numbers Class 10 Maths


Important Questions Class 10 Maths contains all types of questions which could be asked in the examination. We have included short answer questions as well as long answer questions for Chapter 1 Real numbers. For more exercise and practice, students can also refer to the Real Numbers NCERT Solutions. Students can solve these questions and check their answers on the website. All the questions are solved in detail.

Real Numbers Class 10 Maths Important Questions Very Short Answer (1 Mark)


1. For any two integers, the product of the integers = the product of their HCF and LCM. Is this relation true for three or more integers?
Solution

No


2. The decimal expansion of the rational number 43/2453 will terminate after how many places of decimals?

Solution

After 4 decimal places.

3. Write one rational and one irrational number lying between 0.25 and 0.32.
Solution
Given numbers are 0.25 and 0.32.
Clearly,
Thus 0.30 is a rational number lying between 0.25 and 0.32. Also 0.280280028000.....has non-terminating non-repeating decimal expansion. It is an irrational number lying between 0.25 and 0.32

4. Express 98 as a product of its primes.

Solution

2 × 72


5. HCF and LCM of two numbers is 9 and 459 respectively. If one of the numbers is 27, find the other number. (2012)
Solution
We know,
1st number × 2nd number = HCF × LCM
⇒ 27 × 2nd number = 9 × 459
⇒ 2nd number = 9×45927 = 153

6. If HCF(336, 54) 6 = , find LCM(336, 54).
Solution
HCF × LCM = Product of number
6×LCM = 336×54
= 56×54 = 3024
Thus LCM of 336 and 54 is 3024.

7. a and b are two positive integers such that the least prime factor of a is 3 and the least prime factor of b is 5. Then calculate the least prime factor of (a+b).
Solution
Here a and b are two positive integers such that the least prime factor of a is 3 and the least prime factor of b is 5. The least prime factor of (a+b) would be 2.

8. Calculate the HCF of 33×5 and 32×52.
Solution
We have 33×5 = 32×5×3
32×52 = 32×5×5
HCF (33×5, 32×52) = 32 ×5
9×5 = 45

9. Calculate 3/8 in the decimal form.
Solution

10. If HCF (a,b) = 12 and a×b = 1800, then find LCM (a,b).
Solution
HCF (a,b) × LCM (a,b) = a×b
Substituting the values we have
12× LCM (a,b) = 1800

11. Find LCM of numbers whose prime factorisation are expressible as 3 × 52 and 32 × 72. (2014)
Solution
LCM (3×52, 32×72) = 32×52×72
= 9 × 25 × 49
= 11025

12.  Find the least number that is divisible by all numbers between 1 and 10 (both inclusive).
Solution
The required number is the LCM of 1, 2, 3, 4, 5, 6, 7, 8, 9, 10,
LCM = 2×2×3×2×3×5×7 = 2520

Real Numbers Class 10 Maths Important Questions Short Answer-I (2 Marks)


13. Find the LCM of 96 and 360 by using fundamental theorem of arithmetic.
Solution
96 = 25 × 3
360 = 23 × 32 × 5
LCM = 25 × 32 × 5 = 32 × 9 × 5 = 1440

14. Find the largest number which divides 70 and 125 leaving remainder 5 and 8 respectively.
Solution
It is given that on dividing 70 by the required number, there is a remainder 5.
This means that 70 – 5 = 65 is exactly divisible by the required number.
Similarly,
125 – 8 = 117 is also exactly divisible by the required number.
65 = 5 × 13
117 = 32 × 13
HCF = 13
Required number = 13

15. Find HCF and LCM of 404 and 96 and verify that HCF × LCM = Product of the two given numbers.
Solution
404 = 2×2×101
= 22 ×101
96 = 2×2×2×2×2×3
= 25×3
HCF (404, 96) = 22 = 4
LCM (404, 96) = 101×25×3 = 9696
HCF × LCM = 4×9696 = 38784
Also, 404×96 = 38784
Hence, HCF × LCM = Product of 404 and 96

16. Given that HCF (306,1314) = 18. Find LCM 1314
Solution
HCF (306,1314) = 18
LCM (306,1314) = ?
Let a = 306 and b = 1314, then we have
LCM (a,b) × HCF (a,b) = a×b
Substituting values we have,
LCM (a,b)× 18 = 306 × 1314
LCM (306, 1314) = 22,338

17. Complete the following factor tree and find the composite number x.
Solution
z = 371/7 = 53
y = 1855×3 = 5565
x = 2 × y = 2×5565 = 11130
Thus complete factor tree is as given below.

18. Check whether 4n can end with the digit 0 for any natural number n.

Solution

If the number 4n for any n, were to end with the digit zero, then it would be divisible by 5 and 2.

That is, the prime factorization of 4n would contain the prime 5 and 2. This is not possible because the only prime in the factorization of 4n = 22n is 2. So, the uniqueness of the Fundamental Theorem of Arithmetic guarantees that there are no other primes in the factorization of 4n. So, there is no natural number n for which 4n ends with the digit zero. Hence 4n cannot end with the digit zero.


19. Write the denominator of the rational number 257/500 in the form 2m × 5n, where m and n are non-negative integers. Hence write its decimal expansion without actual division.

Solution

500 = 25 × 20

= 52 × 5 × 4

= 53 × 22

Here, denominator is 500 which can be written as 22 × 53.

Now decimal expansion,


20. Write a rational number between √2 and √3.
Solution
We need to find a rational number x such that
Choosing any perfect square such as 225 or 256 in between 200 and 300, we have
Similarly if we choose 256, then we have

21. Can two numbers have 15 as their HCF and 175 as their LCM? Give reasons.
Solution
No,
LCM = Product of the highest power of each factor involved in the numbers.
HCF = Product of the smallest power of each common factor.
We can conclude that LCM is always a multiple of HCF, i.e., LCM = k × HCF
We are given that,
LCM = 175 and HCF = 15
175 = k × 15
⇒ 11.67 = k
But in this case, LCM ≠ k × HCF
Therefore, two numbers cannot have LCM as 175 and HCF as 15.

22. Explain why (17 × 5 × 11 × 3 × 2 + 2 × 11) is a composite number? (2015)
Solution
17 × 5 × 11 × 3 × 2 + 2 × 11 …(i)
= 2 × 11 × (17 × 5 × 3 + 1)
= 2 × 11 × (255 + 1)
= 2 × 11 × 256
Number (i) is divisible by 2, 11 and 256, it has more than 2 prime factors.
Therefore (17 × 5 × 11 × 3 × 2 + 2 × 11) is a composite number.

Real Numbers Class 10 Maths Important Questions Short Answer-II (3 Marks)

23. Prove that 3 + 2√3 is an irrational number.
Solution
Let us assume to the contrary, that 3 + 2√3 is rational.
So that we can find integers a and b (b ≠ 0).
Such that 3 + 2√3 = ab, where a and b are coprime.
Rearranging the equations, we get
Since, a and b are integers, we get a/2b − 3/2 is rational and so √3 is rational.
But this contradicts the fact that √3 is irrational.
So we conclude that 3 + 2√3 is irrational.

24. Prove that 2+√3/5 is an irrational number, given that √3 is an irrational number.
Solution
Assume that 2+√3/5 is a rational number. Therefore, we can write it in the form of p/q where p and q are co-prime integers and q ≠ 0.
Since, p and q are co-prime integers, then 5p-2q/q is a rational number. But this contradicts the fact that √3 is an irrational number. So, our assumption is
wrong. Therefore 2+√3/5 is an irrational number.

25. Write the smallest number which is divisible by both 306 and 657.
Solution
The smallest number that is divisible by two numbers
is obtained by finding the LCM of these numbers
Here, the given numbers are 306 and 657.
306 = 6 × 51 = 3×2×3×17
657 = 9 × 73 = 3×3×73
LCM (306, 657) = 2×3×3×17×73 = 22338
Hence, the smallest number which is divisible by 306 and 657 is 22338.

26. Three bells toll at intervals of 9, 12, 15 minutes respectively. If they start tolling together, after what time will they next toll together?
Solution
9 = 32, 12 = 22 × 3, 15 = 3 × 5
LCM = 22 × 32 × 5 = 4 × 9 × 5 = 180 minutes or 3 hours
They will next toll together after 3 hours.

27. Two tankers contain 850 liters and 680 liters of petrol. Find the maximum capacity of a container which can measure the petrol of each tanker in the exact number of times.
Solution
To find the maximum capacity of a container which can measure the petrol of each tanker in the exact number of times, we find the HCF of 850 and 680.
850 = 2 × 52 × 17
680 = 23 × 5 × 17
HCF = 2 × 5 × 17 = 170
Maximum capacity of the container = 170 liters.

28. 144 cartons of Coke cans and 90 cartons of Pepsi cans are to be stacked in a canteen. If each stack is of the same height and if it equal contain cartons of the same drink, what would be the greatest number of cartons each stack would have?

Solution

The required answer will be HCF of 144 and 90.

144 = 24 × 32

90 = 2 × 32 × 5

HCF (144, 90) = 2 × 32 = 18

Thus each stack would have 18 cartons.


29. If p is prime number, then prove that √p is an irrational.

Solution

Let p be a prime number and if possible, let √p be rational

Thus,

where m and n are co-primes and n ≠0 .

Squaring on both sides, we get

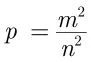
or, pn2 = m2 ...(1)

Here p divides pn2. Thus p divides m2 and in result p also divides m.

Let m = pq for some integer q and putting m = pq in eq. (1), we have

pn2 = p2q2

or, n2 = pq2

Here, p divides pq2. Thus p divides n2 and in result p also divides n.

[∵ p is prime and p divides n2 ⇒ p divides n]

Thus p is a common factor of m and n but this contradicts the fact that m and n are primes. The contradiction arises by assuming that √p is rational.

Hence, √p is irrational.


30. Amita, Sneha, and Raghav start preparing cards for all persons of an old age home. In order to complete one card, they take 10, 16 and 20 minutes respectively. If all of them started together, after what time will they start preparing a new card together? (2013)

Solution

To find the earliest (least) time, they will start preparing a new card together, we find the LCM of 10, 16 and 20.
10 = 2 × 5
16 = 24
20 = 22 × 5
LCM = 24 × 5 = 16 × 5 = 80 minutes
They will start preparing a new card together after 80 minutes.


31. If two positive integers x and y are expressible in terms of primes as x = p2q3 and y = p3q, what can you say about their LCM and HCF. Is LCM a multiple of HCF? Explain. (2014)

Solution

x = p2q3 and y = p3q
LCM = p3q3
HCF = p2q …(i)
Now, LCM = p3q3
⇒ LCM = pq2 (p2q)
⇒ LCM = pq2 (HCF)
Yes, LCM is a multiple of HCF.
Explanation:
Let a = 12 = 22 × 3
b = 18 = 2 × 32
HCF = 2 × 3 = 6 …(ii)
LCM = 22 × 32 = 36
LCM = 6 × 6
LCM = 6 (HCF) [From (ii)]
Here LCM is 6 times HCF.


32. Show that any positive odd integer is of the form 4q + 1 or 4q + 3 where q is a positive integer.
Solution
Let a be a positive odd integer
By Euclid’s Division algorithm:
a = 4q + r …[where q, r are positive integers and 0 ≤ r < 4]
a = 4q
or 4q + 1
or 4q + 2
or 4q + 3
But 4q and 4q + 2 are both even
a is of the form 4q + 1 or 4q + 3.


Real Numbers Class 10 Maths Important Questions Long Answer (4 Marks)

33. Prove that √5 is an irrational number.
Solution
Assume that √5 be a rational number then we have
√5 = a/b
where a and b are co-primes and b≠0.
a = b√5
Squaring both the sides, we have
a2 = 5b2
Thus 5 is a factor of a2 and in result 5 is also a factor of a.
Let a = 5c where c is some integer, then we have
a2 = 25c2
Substituting a2 = 5b2 we have,
5b2 = 25c2
⇒ b2 = 5c2
Thus 5 is a factor of b2 and in result 5 is also a factor of b.
Thus √5 is a common factor of a and b. But this contradicts the fact that a and b are co-primes. Thus, our assumption that √5 is rational number is wrong.
Hence, √5 is irrational.

34. Prove that n2 - n is divisible by 2 for every positive integer n.

Solution

We have n2 - n = n(n-1)
Thus n2 - n is product of two consecutive positive integers.
Any positive integer is of the form 2q or 2q + 1, for some integer q.
Case 1: n = 2q
If n = 2q we have
n(n-1) = 2q(2q-1)
= 2m
where m = q(2q-1) which is divisible by 2.
Case 2: n = 2q+1
If n = 2q+1, we have
n(n-1) = (2q+1) (2q+1-1)
= 2q(2q+1)
= 2m
where m = q(2q+1) which is divisible by 2.
Hence, n2 - n is divisible by 2 for every positive
integer n.


Real Numbers Class 10 Maths Case Based Questions

A. Read the following text and answer the following questions on the basis of the same:

To enhance the reading skills of grade X students, the school nominates you and two of your friends to set up a class library. There are two sections- section A and section B of grade X. There are 32 students in section A and 36 students in section B.

1. If p and q are positive integers such that p = ab2 and q = a2b, where a, b are prime numbers, then the LCM (p, q) is

A. ab

B. a3b3

C. a3b2

D. a2b2

Solution

D. a2b2

Given, p = ab2 = a × b × b

q = a2b = a × a × b

LCM of (p, q) = a2b2


2. If the product of two positive integers is equal to the product of their HCF and LCM is true then, the HCF (32 , 36) is

A. 2

B. 4

C. 6

D. 8

Solution

B. 4

Prime factor 32 is 2×2×2×2×2

Prime factor 36 is 2×2×3×3

HCF is 2×2 = 4

HCF of 32 and 36 is 4.


3. 7 × 11 × 13 × 15 + 15 is a

A. Prime number
B. Composite number
C. Neither prime nor composite
D. None of the above

Solution

B. Composite number

7 × 11 × 13 × 15 + 15 is composite number.

Take 15 common

15 ( 7 × 11 × 13 + 1)

So, given number has factor other than 1 and itself so it is a composite number.


4. What is the minimum number of books you will acquire for the class library, so that they can be distributed equally among students of Section A or Section B?

A. 144
B. 128
C. 288
D. 272

Solution

We have to find the LCM of 32 and 36.

LCM(32, 36) = 25 × 9 = 288

Hence, the minimum number of books required to distribute equally among students of section A and section B are 288.


B. Read the following text and answer the following questions on the basis of the same:

A garden consists of 135 rose plants planted in certain number of columns. There are another set of 225 marigold plants, which is to be planted in the same number of columns.

1. Find the sum of exponents of the prime factors of total number of plants.

A. 2
B. 3
C. 5
D. 6

Solution

D. 6

Total number of plants = 135 + 225 = 360

The prime factors of 360 = 2 × 2 × 2 × 3 × 3 × 5

= 23 × 32 × 51

∴ Sum of exponents = 3 + 2 + 1 = 6.


2. What is total numbers of row in which they can be planted

A. 3
B. 5
C. 8
D. 15

Solution

C. 8

Number of rows of Rose plants = 135/45 = 3

Number of rows of marigold plants = 225/45 = 5

Total number of rows = 3 + 5 = 8


3. Find the sum of exponents of the prime factors of the maximum number of columns in which they can be planted.

A. 5

B. 3

C. 4

D. 6

Solution

We have proved that the maximum number of columns = 45

So, prime factors of 45

= 3 × 3 × 5 = 32 × 51

∴ Sum of exponents = 2 + 1 = 3.


More Study Materials for Class 10

أحدث أقدم