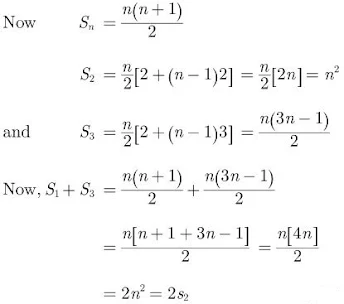Important Questions for Class 10 Maths Chapter 5 Arithmetic Progressions

Chapter 5 Arithmetic Progressions Important Questions for CBSE Class 10 Maths Board Exams

This page contains Important Questions for Class 10 Maths Chapter 5 Arithmetic Progressions, which will help the students to prepare for the CBSE Class 10 maths Board exam 2022-23. It help the doing better in their maths paper. Extra questions of Chapter 5 Arithmetic Progressions given here which are based on the pattern of CBSE NCERT book. Students will learn about the entire syllabus and learn how to solve problems in preparation for the exams.

Important Questions for Chapter 5 Arithmetic Progressions Class 10 Maths

Important Questions Class 10 Maths contains all types of questions which could be asked in the examination. We have included short answer questions as well as long answer questions for Chapter 5 Arithmetic Progressions. For more exercise, students can also refer to the Arithmetic Progressions NCERT Solutions. Students can solve these questions and check their answers on the website. All the questions are solved in detail.

Arithmetic Progressions Class 10 Maths Important Questions Very Short Answer (1 Mark)

1. The sum of first 20 terms of the AP 1, 4, 7, 10 .... is

Solution

Given AP is 1, 4, 7, 10 ...

Here, a = 1, d = 4 - 1 = 3 and n = 20

= 10(2+57) = 10×59 = 590

2.  If 4 times the 4th term of an AP is equal to 18 times the 18th term, then find the 22 nd term.

Solution

Let a be the first term and d be the common difference of the AP.

Now,

a_n = a + (n-1)d

As per the information given in question

4 × a₄ = 18 × a₁₈

⇒ 4(a+3d) = 18(a+17d)

⇒ 2a + 6d = 9a + 153d

⇒ 7a = -147d

⇒ a = -21d

⇒ a + 21d  = 0

⇒ a + (22-1)d = 0

⇒ a₂₂ = 0

Hence, the 22nd term of the AP is 0.

3. Find the sum of all 11 terms of an AP whose middle term is 30.

Solution

In an AP with 11 terms, the middle term is 11+1/2 = 6th term.

Now,

a₆ = a + 5d = 30

= 11(a+5d)

= 11×30 = 330

4. If the first three terms of an AP are b, c and 2b, then find the ratio of b and c.

Solution

Given, b, c and 2b are in AP.

Thus,

c - b = 2b - c

⇒ 2c = 3b

5. Find the 9th term from the end (towards the first term) of the A.P. 5,9,13, …, 185.

Solution

Here,
First term, a = 5
Common difference, d = 9 – 5 = 4
Last term, 1 = 185
n^th term from the end = l – (n – 1)d
9^th term from the end = 185 – (9 – 1)4
= 185 – 8 × 4
= 185 – 32
= 153

6. Find the common difference of the AP 1/p, 1−p/p, 1−2p/p,…

Solution

The common difference,

7. What is the common difference of an A.P. in which a₂₁ – a₇ = 84?

Solution

a₂₁ – a₇ = 84 …[Given]

∴ (a + 20d) – (a + 6d) = 84 …[a_n = a + (n – 1)d]

⇒ 20d – 6d = 84

⇒ 14d = 84

⇒ d = 84/14 = 6

8. Find, how many two digit natural numbers are divisible by 7.

Solution

Two digits number which are divisible by 7 form an

AP given by 14, 21, 28, ..., 98

Here,

a = 14, d = 21-14 = 7 and a_n = 98

Now,

a_n = a + (n – 1)d

98 = 14 + (n-1)7

⇒ 98 - 14 = 7n - 7

⇒ 91 = 7n

⇒ n = 13

Hence, there are 13 numbers divisible by 7.

9. Which of the term of AP 5, 2, ,...... 1 - is 49 - ?

Solution

Let the first term of an AP be a and common difference d.

We have,

a = 5, d = 3

Now,

a_n = a + (n – 1)d

Substituting all values we have

-49 = 5+(n-1)(-3)

⇒ -49 = 5 - 3n + 3

⇒ 3n = 49 + 5 + 3

⇒ n = 57/3 = 19th term

10. If the common difference of an AP is -6, find a₁₆ - a₁₂.

Solution

Let the first term of an AP be a and common difference be d.

Now,

d= -6

a₁₆ = a + (16-1)(-6) = a - 90

a₁₂ = a + (12-1)(-6) = a - 66

a₁₆ - a₁₂ = (a-90) - (a-66)

= a - 90 - n + 66 = -24

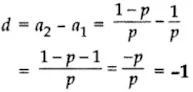
Arithmetic Progressions Class 10 Maths Important Questions Short Answer-I(2 Marks)

11. Which term of the progression 4, 9, 14, 19, … is 109? (2011D)

Solution

Here,
d = 9 - 4 = 14 -9 = 19 – 14 = 5
∴ Difference between consecutive terms is constant.
Hence, it is an A.P.

Given,
First term, a = 4, d = 5, a_n = 109 (Let)
∴ a_n = a + (n – 1) d …[General term of A.P.]
∴ 109 = 4 + (n – 1) 5
⇒ 109 – 4 = (n – 1) 5
⇒ 105 = 5(n − 1)
⇒ n – 1 = 105/5 = 21
⇒ n = 21 + 1 = 22
∴ 109 is the 22^nd term

12. Find the sum of first ten multiple of 5.

Solution

Let the first term be a, common difference be d, nth term be a_n and sum of n term be S_n.

Here,

a = 5, n = 10, d = 5

= 5[10+ 9×5]

= 5[10+45]

= 5×55 = 275

Hence, the sum of first ten multiple of 5 is 275.

13. If the sum of first m terms of an AP is the same as the sum of its first n terms, show that the sum of its first (m+n) terms is zero.

Solution

Let a be the first term and d be the common difference of the given AP.

Then,

S_m = S_n

14. If 3k-2, 4k-6 and k+2 are three consecutive terms of AP, then find the value of k.

Solution

To be term of an AP the difference between two

consecutive terms must be the same.

If 3k-2, 4k-6 and k+2 are terms of an AP, then

4k -6 -(3k-2) = k + 2 - (4k-6)

⇒ 4k - 6 -3k + 2 = k + 2 -4k + 6

⇒ k - 4 = 8 - 3k

⇒ 4k = 12

⇒ k = 3

Hence, the value of k is 3.

15. How many terms of AP 3, 5, 7, 9, ..... must be taken to get the sum 120?

Solution

Given,

AP : 3, 5, 7, 9, ...

We have a = 3, d = 2 and S_n = 120

120 = n(3+n - 1)

⇒ 120 = n(n+2)

⇒ n² + 2n - 120 = 0

⇒ n² + 12n - 10n - 120 = 0

⇒ (n + 12) (n - 10) = 0

⇒ n = 10 or n = -12

Neglecting n = -12 because n can’t be negative we get n = 10. Hence, 10 terms must be taken to get the sum 120.

16. Which term of the AP 3, 15, 27, 39, ... will be 120 more than its 21st term?

Solution

Given,

AP is 3, 15, 27, 39......

Here, first term, a 3 = and common difference, d = 12

Now,

21st term of AP is

a_n = a + (n-1)d

a₂₁ = 3 + (21-1) 12

= 3+ 20×12

= 3+ 240

= 243

Therefore, 21st term is 243.

Now, we need to calculate term which is 120 more than 21st term i.e. it should be 243 + 120 = 363

Therefore,

a_n = a + (n – 1) d

363 = 3 + (n-1)12

⇒ 360 = 12(n-1)

⇒ n - 1 = 30

⇒ n  = 31

So, 31st term is 120 more than 21st term.

17. Find the 21st term of the AP -4 1/2, -3, -1 1/2, ....

Solution

18. The 4^th term of an A.P. is zero. Prove that the 25th term of the A.P. is three times its 11^thterm.

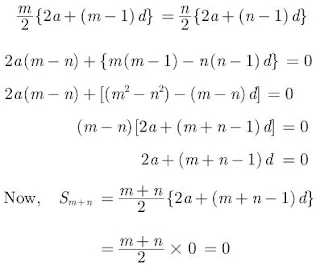
Solution

Let 1^st term = a, Common difference = d
a₄ = 0 a + 3d = 0
⇒ a = -3d …(i)
To prove: a₂₅ = 3 × a₁₁
a + 24d = 3(a + 10d) …[From (i)]
⇒ -3d + 24d = 3(-3d + 10d)
⇒ 21d = 21d
From above, a₂₅ = 3(a₁₁)

19. Find 10th term from end of the A.P. 4,9, 14, …, 254. (2011OD)

Solution

Common difference d = 9 – 4
= 14 – 9 = 5
Given: Last term, l = 254, n = 10
n^th term from the end = l – (n – 1) d
∴ 10^th term from the end = 254 – (10 – 1) × 5
= 254 – 45 = 209

20. Find, 100 is a term of the AP 25, 28, 31,....  or not.

Solution

Let the first term of an AP be a, common difference

be d and number of terms be n.

Let a_n = 100

Here, a = 25, d = 28-25 = 31-28 = 3

Now,

a_n = a + (n-1)d,

100 = 25 + (n-1) 3

⇒ 100 - 25 = 75 = (n-1) 3

⇒ 25 = n - 1

⇒ n  = 26

Since, 26 is an whole number, thus 100 is a term of given A.P.

21. Find the 7th term from the end of AP 7, 10, 13,.... 184

Solution

Let us write AP in reverse order i.e., 184, .....13, 10, 7

Let the first term of an AP be a and common

difference be d.

Now,

d = 7-10 = -3

a = 184, n = 7

7th term from the original end.

a₇  = a +6d

⇒ a₇ = 184 + 6(-3)

= 184 -18 = 166

Hence, 166 is the 7th term from the end.

22. Which term of an AP 150, 147, 144, ..... is its first negative term?

Solution

Let the first term of an AP be a, common difference be d and nth term be a_n.

For first negative term,

a_n < 0

⇒ a + (n-1)d < 0

⇒ 150 + (n-1)(-3) < 0

⇒ 150 - 3n + 3 < 0

⇒ -3n < -153

⇒ n > 51

Therefore, the first negative term is 52 nd term.

23. The seventeenth term of an AP exceeds its 10th term by 7. Find the common difference.

Solution

Let the first term be a and common difference be d.

Now,

a₁₇ = a₁₀ + 7

⇒ a + 16d = a + 9d + 7

⇒ 16d - 9d = 7

⇒ 7d = 7

⇒ d = 1

Thus common difference is 1.

24. The first and the last terms of an AP are 5 and 45 respectively. If the sum of all its terms is 400, find its common difference.

Solution

Here, a_n = 45, S_n = 400, a = 5, n = ?, d = ?

25. How many terms of the AP 65, 60, 55.... 65 60 55 be taken so that their sum is zero?

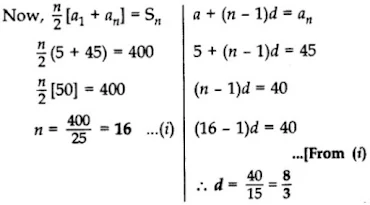
Solution

Let the first term be a, common difference be d, nth term be a n and sum of n term be Sn .

We have, a = 65, d = -5, S_n = 0

⇒ 135n - 5n² = 0

⇒ n(135 - 5n) = 0

⇒ 5n = 135

⇒ n = 27

26. How many terms of the AP 18, 16, 14.... be taken so that their sum is zero?

Solution

Let the first term be a, common difference be d, nth term be an and sum of n term be S_n.

Here,

a = 18, d = -2, S_n = 0

27. The first and last term of an AP are 5 and 45 respectively. If the sum of all its terms is 400, find its common difference.

Solution

Let the first term be a, common difference be d, nth term be a n and sum of n term be S_n.

We have,

a = 5, an = 45

Now,

45 = 5 + (n-1)d

⇒ (n-1)d = 40

Given,

S_n = 400

28. Find the sum of all three digit natural numbers, which are multiples of 11.

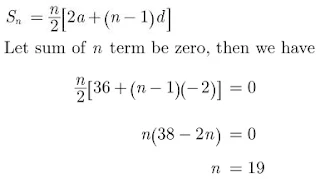
Solution

To find: 110 + 121 + 132 + … + 990
Here,
a = 110, d = 121- 110 = 11, a_n = 990
∴ a + (n – 1)d = 990
110 + (n – 1).11 = 990
⇒ (n – 1). 11 = 990 – 110 = 880
⇒ (n – 1) = 880 = 80
⇒ n = 80 + 1 = 81
As,
S_n = n/2 (a₁ + a_n)
∴ S₈₁ = 81/2 (110 + 990)
= 81/2 (1100) = 81 × 550 = 44,550

29. Find how many integers between 200 and 500 are divisible by 8.

Solution

Number divisible by 8 are 208, 2016, 224, .... 496. It is an AP

Let the first term be a, common difference be d and nth term be a_n.

We have a = 208, d = 8, a_n = 496

Now,

a + (n-1)d = a_n

⇒ 208 + (n-1)d = 496

⇒ (n-1)8 = 496 - 208

⇒ n = 36+1 = 37

Hence, required numbers divisible by 8 is 37.

30. The fifth term of an AP is 26 and its 10th term is 51. Find the AP

Solution

Let the first term be a, common difference be d and nth term be a_n.

a₅ = a + 4d = 26 ...(1)

a₁₀ = a + 9d = 51 ...(2)

Subtracting (1) from (2) we have

5d = 25

⇒ d = 5

Substituting this value of d in equation (1) we get

a = 6

Hence, the AP is 6, 11, 16, ....

32. Find whether -150 is a term of the AP 11, 8, 5, 2, ...

Solution

Let the first term be a, common difference be d and nth term be a_n.

Let the nth term of given AP 11, 8, 5, 2... be -150

Hence,

a = 11, d = 8-11 = -3 and an = -150

a + (n-1)d = an

⇒ 11 + (n-1)(-3) = -150

⇒ (n-1)(-3) = -161

which is not a whole number. Hence -150 is not a term of given AP.

Arithmetic Progressions Class 10 Maths Important Questions Short Answer-II (3 Marks)

33. The sum of the first 7 terms of an AP is 63 and that of its next 7 terms is 161. Find the AP.

Solution

We have,

S₇ = 63

Subtracting equation (1) from (2) we have

14 = 7d

⇒ d = 2

Substituting the value of d in (1), we get

a = 3

Hence, the AP is 3, 5, 7, 9 ...

34. The sum of four consecutive number in AP is 32 and the ratio of the product of the first and last term to the product of two middle terms is 7 : 15. Find the numbers.

Solution

Let the four consecutive terms of AP be (a-3d), (a-d), (a+d) and (a+3d)

As per question statement we have

a-3d + a-d + a+d + a+3d = 32

⇒ 4a = 32

⇒ a = 8

Hence, the number are 2, 6, 10 and 14 or 14, 10, 6 and 2.

35. Which term of the A.P. 3, 14, 25, 36,… will be 99 more than its 25th term?

Solution

Let the required term be n^th term, i.e., a_n
Here,
d = 14 – 3 = 11, a = 3
According to the Question,
a_n = 99 + a₂₅
∴ a + (n – 1) d = 99 + a + 24d
⇒ (n – 1) (11) = 99 + 24 (11)
⇒ (n – 1) (11) = 11 (9 + 24)
⇒ n – 1 = 33
⇒ n = 33 + 1 = 34
∴ 34^th term is 99 more than its 25th term.

36. Which term of the AP 20, 19 1/4, 18 1/2, 17 3/4, ...is the first negative term.

Solution

Here,

a = 20

n = 28

Hence, the first negative term is 28th term.

37. If in an AP, the sum of first m terms is n and the sum of its first n terms is m, then prove that the sum of its first (m+n) terms is -(m+n)

Solution

Let 1st term of series be a and common difference be d, then we have

S_m = n

S_n = m

38. Find the 20th term of an AP whose 3rd term is 7 and the seventh term exceeds three times the 3rd term by 2. Also find its nth term (a_n).

Solution

Let the first term be a, common difference be d and

nth term be an.

We have,

a₃ = a+2d = 7 ...(1)

a₇ = 3a3 + 2

⇒ a+6d = 3×7 +2 = 23 ...(2)

Solving (1) and (2) we have

4d = 16

⇒ d = 4

a+8 = 7

⇒ a = -1

a₂₀ = a+19d = -1 + 19×4 = 75

a_n = a+(n-1)d

= -1 + 4n - 4

= 4n - 5

Hence nth term is 4n - 5.

39. If 7th term of an AP is 1/9 and 9th term is 1/7, find 63rd term.

Solution

Let the first term be a, common difference be d and nth term be a_n.

40. The 19th term of an AP is equal to three times its 6^th term. If its 9^th term is 19, find the A.P.

Solution

Given,
a₁₉ = 3(a₆)
⇒ a + 18d = 3(a + 5d)
⇒ a + 18d = 3a + 15d
⇒ 18d – 15d = 3a – a

41. The sum of the 5th and the 9th terms of an AP is 30. If its 25^th term is three times its 8^th term, find the AP.

Solution

a₅ + a₉ = 30 …[Given]
⇒  a + 4d + a + 8d = 30 …[∵a_n = a + (n – 1)d]
⇒  2a + 12d = 30
⇒ a + 6d = 15 …[Dividing by 2]
⇒  a = 15 – 6d …(i)
Now, a₅₂ = 3(a₈)
a + 24d = 3(a + 7d)
⇒ 15 – 6d + 240 = 3(15 – 6d + 7d) …[From (i)]
⇒ 15 + 18d = 3(15 + d)
⇒ 15 + 18d = 45 + 3d
⇒ 18d – 3d = 45 – 15
⇒ 15d = 30
∴ d = 30/15 = 2
From (i), a = 15 – 6(2) = 15 – 12 = 3

42.  The ninth term of an AP is equal to seven times the second term and twelfth term exceeds five times the third term by 2. Find the first term and the common difference.

Solution

Let the first term be a, common difference be d and nth term be a_n.

Now,

a₉ = 7a₂

⇒ a + 8d = 7(a+d)

⇒ a + 8d = 7a + 7d

⇒ -6a + d = 0 ...(1)

and

a₁₂ = 5a₃ + 2

⇒ a + 11d = 5(a+2d) + 2

⇒ a + 11d = 5a + 10d + 2

⇒ -4a + d = 2 ...(2)

Subtracting (2) from (1), we get

-2a = -2

⇒ a = 1

Substituting this value of a in equation (1) we get

-6 + d = 0

⇒ d = 6

Hence first term is 1 and common difference is 6.

43. The sum of first n terms of three arithmetic progressions are S₁, S₂ and S₃ respectively. The first term of each AP is 1 and common differences are 1, 2 and 3 respectively. Prove that S₁ + S₃ = 2S₂.

Solution

Let the first term be a, common difference be d, nth term be an and sum of n term be Sn.

We have,

S₁ = 1+2+3+ ... n

S₂ = 1+3+5+ ... up to n terms

S₃ = 1+4+7+ ... upto n terms

44. If Sn denotes, the sum of the first n terms of an AP prove that S₁₂ = 3(S₈ - S₄).

Solution

Let the first term be a, common difference be d, nth term be a n and sum of n term be S_n.

45. Find the number of terms of the AP 18, 15 1/2, 13,…, -49 1/2 and find the sum of all its terms.

Solution

Here 1^st term, a = 18

46. If the ratio of the sums of first n terms of two AP’s is (7n + 1): (4n + 27), find the ratio of their nth terms.

Solution

Let a and A be the first term and d and D be the common difference of two AP’s, then we have

47. The first term of an A.P. is 5, the last term is 45 and the sum of all its terms is 400. Find the number of terms and the common difference of the A.P.

Solution

First term, a = 5, Last term, a_n = 45
Let the number of terms = n
S_n = 400
⇒ n/2 (a + a_n) = 400
⇒ n/2(5 + 45) = 400
⇒ n/2 (50) = 400
⇒ n = 400/25 = 16 = Number of terms
Now, a_n = 45
a + (n – 1)d = a_n
⇒ 5+ (16 – 1)d = 45
⇒ 15d = 45 – 5
∴ d = 40/15=8/3

48. The sum of first n terms of an AP is 3n² + 4n. Find the 25^th term of this AP.

Solution

We have, S_n = 3n² + 4n
Put n = 25,
S₂₅ = 3(25)² + 4(25)
= 3(625) + 100
= 1875 + 100 = 1975
Put n = 24,
S₂₄ = 3(24)² + 4(24)
= 3(576) + 96
= 1728 + 96 = 1824
∴ 25^th term = S₂₅ – S₂₄
= 1975 – 1824 = 151

49. The digits of a positive number of three digits are in A.P. and their sum is 15. The number obtained by reversing the digits is 594 less than the original number. Find the number.

Solution

Let hundred’s place digit = (a – d)
Let ten’s place digit = a
Let unit’s place digit = a + d
According to the Question,
a – d + a + a + d = 15
⇒ 3a = 15
⇒ a = 5
Original number
= 100(a – d) + 10(a) + 1(a + d)
= 100a – 100d + 10a + a + d
= 111a – 99d
Reversed number
= 1(a – d) + 10a + 100(a + d)
= a – d + 10a + 100a + 100d
= 111a + 99d
Now, Original no. – Reversed no. = 594
111a – 99d – (111a + 99d) = 594
-198d = 594
⇒ d = 594/-198 = -3
∴ The Original no. = 111a – 99d
= 111(5) – 99(-3)
= 555 + 297 = 852

50. Find the sum of all multiples of 7 lying between 500 and 900. (2012OD)

Solution

To find: 504 + 511 + 518 + … + 896
a = 504, d = 511- 504 = 7, a_n = 896
a + (n – 1)d = a_n
∴ 504 + (n – 1)7 = 896
(n – 1)7 = 896 – 504 = 392

51. The tenth term of an AP, is -37 and the sum of its first six terms is -27. Find the sum of its first eight terms.

Solution

Let the first term be a, common difference be d, nth

term be a n and sum of n term be Sn.

a_n = a + (n-1)d

a + 9d = -37 ...(1)

⇒ 3 (2a + 5d) = -27

⇒ 2a + 5d = -9 ...(2)

Multiplying (1) by 2 and subtracting (2) from it, we

get

(2a + 18d) - (2a + 5d) = -74 + 9

⇒ 13d = -65

⇒ d = -5

Substituting the value of d in (1) we get

a + 9×-5 = -37

⇒ a = -37 + 45

⇒ a = 8

Hence, S_n = -76

52. The 16th term of an AP is five times its third term. If its 10th term is 41, then find the sum of its first fifteen terms.

Solution

Let the first term be a, common difference be d, nth

term be a n and sum of n term be S n .

We have,

a₁₆ = 5a₃

⇒ a + 15d = 5(a + 2d)

⇒ 4a = 5d ...(1)

and a10 = 41

a + 9d = 41 ...(2)

Solving (1) and (2), we get a = 5, d = 4

Now,

Thus, S₁₅ = 495

53. Find the sum of n terms of the series

(4 - 1/n) + (4 - 2/n) + (4 - 3/n) +....

Solution

Let sum of n term be S_n

54. Find the number of natural numbers between 101 and 999 which are divisible by both 2 and 5.

Solution

The sequence goes like 110, 120, 130, ...... 990

Since they have a common difference of 10, they form an AP. Let the first term be a, common difference be d, nth term be S_n.

Here,

a = 110, a_n = 990, d = 10

a_n = a + (n - 1)d

⇒ 990 = 110 + (n - 1) 10

⇒ 990 - 110 = 10(n - 1)

⇒ 880 = 10(n - 1)

⇒ 88 = n - 1

⇒ n = 88 + 1 = 89

Hence, there are 89 terms between 101 and 999 divisible by both 2 and 5.

55. If the ratio of the 11th term of an AP to its 18th term is 2 : 3, find the ratio of the sum of the first five term of the sum of its first 10 terms.

Solution

Let the first term be a, common difference be d, nth term be a n and sum of n term be S_n

Hence, S₅ : S₁₀ = 6:17

Arithmetic Progressions Class 10 Maths Important Questions Long Answer (4 Marks)

56. The first term of an AP is 3, the last term is 83 and the sum of all its terms is 903. Find the number of terms and the common difference of the AP.

Solution

First term, a = 3

Last term, a_n = 83

Sum of n terms, S_n = 903

Hence, the common difference is 4.

57. Find the common difference of the Arithmetic Progression 1/a, 3-a/3a, 3-2a/3a, ... (a≠0)

Solution

58. f p^th, q^th and r^th terms of an A.P. are a, b, c respectively, then show that (a – b)r + (b – c)p+ (c – a)q = 0.

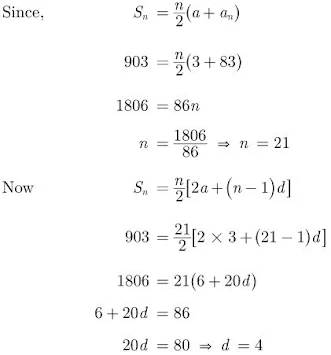
Solution

Let A be the first term and D be the common difference of the given A.P.
p^th term = A + (p – 1)D = a …(i)
q^th term = A + (q – 1)D = b …(ii)
r^th term = A + (r – 1)D = c …(iii)
L.H.S. = (a – b)r + (b – c)p + (c – a)q
= [A + (p – 1)D – (A + (q – 1)D)]r + [A + (q – 1)D – (A + (r – 1)D)]p + [A + (r – 1)D – (A + (p – 1)D)]q
= [(p – 1 – q + 1)D]r + [(q – 1 – r + 1)D]p + [(r – 1 – p + 1)D]q
= D[(p – q)r + (q – r)p + (r – p)q]
= D[pr – qr + qp – rp + rq – pq]
= D[0] = 0 = R.H.S.

59. A sum of ₹1,600 is to be used to give ten cash prizes to students of a school for their overall academic performance. If each prize is ₹20 less than its preceding prize, find the value of each of the prizes.

Solution

Here,
S₁₀ = 1600, d = -20, n = 10
S_n = n/2 (2a + (n – 1)d]
∴ 10/2[2a + (10 – 1)(-20)] = 1600
2a – 180 = 320
2a = 320 + 180 = 500
a = 250
∴ 1^st prize = a = ₹250
2^nd prize = a₂ = a + d = 250 + (-20) = ₹230
3^rd prize = a₃ = a₂ + d = 230 – 20 = ₹210
4^th prize = a₄ = a₃ + d = 210 – 20 = ₹190
5^th prize = a₅ = a₄ + d = 190 – 20 = ₹170
6^th prize = a₆ = a₅ + d = 170 – 20 = ₹150
7^th prize = a₇ = a₆ + d = 150 – 20 = ₹130
8^th prize = a₈ = a₇ + d = 130 – 20 = ₹110
9^th prize = a₉ = a₈ + d = 110 – 20 = ₹590
10^th prize = a₁₀ = a₉ + d = 90 – 20 = ₹70
= ₹1,600

60. If the sum of first four terms of an AP is 40 and that of first 14 terms is 280. Find the sum of its first n terms.

Solution

Let a be the first term and d be the common difference.

Sum of n terms of an AP,

Hence, sum of n terms is 6n + n².

61. If Sn denotes the sum of first n terms of an AP, prove that, S₃₀ = 3(S₂₀ - S₁₀)

Solution

Let the first term be a, and common difference be d.

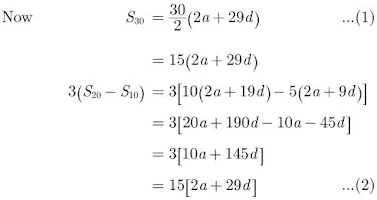
Hence, S₃₀ = 3(S₂₀ - S₁₀)

62. Find the 60th term of the AP 8, 10, 12,.... if it has a total of 60 terms and hence find the sum of its last 10 terms.

Solution

Let the first term be a, common difference be d, nth term be a n and sum of n term be S_n

We have,

a = 8, d = 10 - 8 = 2

a_n = a + (n-1)d

Now,

a₆₀ = 8 + (60 - 1)2

= 8+ 59×2 = 126

and a₅₁ = 8 + 50×2

= 8 + 100 = 108

Sum of last 10 terms,

Hence sum of last 10 terms is 1170.

63. An AP consists of 37 terms. The sum of the three middle most terms is 225 and the sum of the past three terms is 429. Find the AP.

Solution

Let the middle most terms of the AP be (x-d), x and (x+d).

We have,

x-d + x + x+d = 225

⇒ 3x = 225

⇒ x = 75

and the middle term = 37+1/2 = 19th term.

Thus AP is,

(x-18d),...(x-2d), (x-d), x, (x+d), (x+2d),...(x+18d)

Sum of last three terms,

(x+18d) + (x+17d) + (x+16d) = 429

⇒ 3x + 51d = 429

⇒ 225 + 51d = 429

⇒ d = 4

First term, a₁ = x-18d = 75- 18×4 = 3

a₂ = 3+4 = 7

Hence, AP = 3, 7, 11,...,147.

64. The first and the last terms of an A.P. are 8 and 350 respectively. If its common difference is 9, how many terms are there and what is their sum?

Solution

Here,
a = 8, a_n = 350, d = 9
As we know, a + (n − 1) d = a₂
∴ 8 + (n – 1) 9 = 350
⇒ (n − 1) 9 = 350 – 8 = 342
⇒ n – 1 = 342/9 = 38
⇒ n = 38 + 1 = 39
∴ There are 39 terms.
∴ S_n = n/2(a + an)
∴ S₃₉ = 39/2 (8 + 350) = 39/2 × 358
= 39 × 179 = 6981

65. In an AP of 50 terms, the sum of first 10 terms is 210 and the sum of its last 15 terms is 2565. Find the AP.

Solution

Here,
n = 50,
S₁₀ = 210
= 10/2 (2a + 9d) = 210 …[S_n = 1/2 [2a+(n – 1)2]
⇒ 5(2a + 9d) = 210
⇒ 2a + 9d = 210/5 = 42
⇒ 2a = 42 – 9d
⇒ a = 42−9d/2 …(i)
Now,
50 = (1 + 2 + 3 + …) + (36 + 37 + … + 50) Sum = 2565
Sum of its last 15 terms = 2565 …(Given)
S₅₀ – S₃₅ = 2565
⇒ 50/2(2a + 49d) – 35/2 (2a + 34d) = 2565
⇒ 100a + 2450d – 70a – 1190d = 2565 × 2
⇒ 30a + 1260d = 5130
⇒ 3a + 1260 = 513 …(Dividing both sides by 10)

66. In a school, students decided to plant trees in and around the school to reduce air pollution. It was decided that the number of trees, that each section of each class will plant, will be double of the class in which they are studying. If there are 1 to 12 classes in the school and each class has two Sections, find how many trees were planted by the students.

Solution

Classes: 1 + I + II + … + XII
Sections: 2(I) + 2(II) + 2(III) + … + 2(XII)
Total no. of trees
= 2 + 4 + 6 … + 24
= (2 × 2) + (2 × 4) + (2 × 6) + … + (2 × 24)
= 4 + 8 + 12 + … + 48
:: S₁₂ = 12/2(4 + 48) = 6(52) = 312 trees

67. Find the sum of first 24 terms of an AP whose nth term is given by an = 3+2n

Solution

Let the first term be a, common difference be d, nth term be an and sum of n term be Sn

We have,

a_n = 3+2n

a₁ = 3+ 2×1 = 5

a₂ = 3 + 2×2 = 7

a₃ = 3 + 2×3 = 9

Thus, the series is 5, 7, 9,... in which

a = 5 and d = 2

Now,

Hence, S₂₄ = 672

68. Ramkali required ₹500 after 12 weeks to send her daughter to school. She saved ₹100 in the first week and increased her weekly saving by ₹20 every week. Find whether she will be able to send her daughter to school after 12 weeks.

Solution

Money required by Ramkali for admission of her daughter = ₹2500
A.P. formed by saving
100, 120, 140, … upto 12 terms …(i)
Let, a, d and n be the first term, common difference and number of terms respectively.
Here,
a = 100, d = 20, n = 12
S_n = n/2 (2a + (n − 1)d)
⇒ S₁₂ = 12/2 (2(100) + (12 – 1)20)
⇒ S₁₂ = 12/2 [2(100) + 11(20)] = 6[420] = ₹2520

69. How many multiples of 4 lie between 10 and 250? Also find their sum. (2011D)

Solution

Multiples of 4 between 10 and 250 are:
12, 16, 20, … 248
Here, a = 12, d = 4, a_n = 248
As we know, a + (n – 1) d = a_n
∴12 + (n – 1) 4 = 248
⇒ (n – 1) 4 = 248 – 12 = 236
⇒ n – 1 = 236/4 = 59
⇒ n = 59 + 1 = 60
∴ There are 60 terms.
Now, S_n = n2 (a + a_n)
∴ S₆₀ = 60/2(12 + 248)
= 30 (260) = 7800

70. The houses in a row are numbered consecutively from 1 to 49. Show that there exists a value of X such that sum of numbers of houses preceding the house numbered X is equal to sum of the numbers of houses following X.

Solution

Here,
A.P. is 1, 2, 3, …., 49
a = 1, d = 1, a_n = 49

Now,
⇒ (X – 1)² (2 + (X – 2)) = 49(2 + 48) – X[2 + (x – 1)]
⇒ (X – 1). X = 2,450 – X(X + 1)
⇒ x² – X = 2,450 – X² – X
⇒ X² – X + X² + X = 2,450
⇒ 2X² = 2,450
⇒ X² = 1,225
∴ X = √1225 = 35 …[X can not be -ve]

More Study Materials for Class 10

• Important Questions Class 10
• NCERT Solutions Class 10 Maths
• Important Questions Class 10 Maths
• Study Materials for Class 10 Maths
• Maths Formula Class 10
• Solved MCQ Questions Class 10