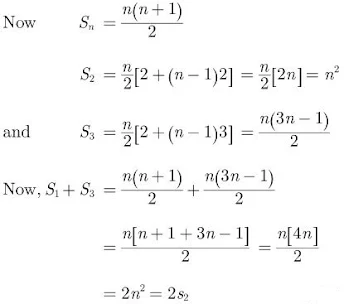Chapter 5 Arithmetic Progressions Important Questions for CBSE Class 10 Maths Board Exams

Important Questions for Chapter 5 Arithmetic Progressions Class 10 Maths
Arithmetic Progressions Class 10 Maths Important Questions Very Short Answer (1 Mark)


Solution
Here,
First term, a = 5
Common difference, d = 9 – 5 = 4
Last term, 1 = 185
nth term from the end = l – (n – 1)d
9th term from the end = 185 – (9 – 1)4
= 185 – 8 × 4
= 185 – 32
= 153
6. Find the common difference of the AP 1/p, 1−p/p, 1−2p/p,…
Solution
The common difference,
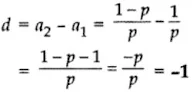
Arithmetic Progressions Class 10 Maths Important Questions Short Answer-I(2 Marks)
Solution
Here,
d = 9 - 4 = 14 -9 = 19 – 14 = 5
∴ Difference between consecutive terms is constant.
Hence, it is an A.P.
Given,
First term, a = 4, d = 5, an = 109 (Let)
∴ an = a + (n – 1) d …[General term of A.P.]
∴ 109 = 4 + (n – 1) 5
⇒ 109 – 4 = (n – 1) 5
⇒ 105 = 5(n − 1)
⇒ n – 1 = 105/5 = 21
⇒ n = 21 + 1 = 22
∴ 109 is the 22nd term
12. Find the sum of first ten multiple of 5.
Solution
Let the first term be a, common difference be d, nth term be an and sum of n term be Sn.
Here,
a = 5, n = 10, d = 5

= 5[10+ 9×5]
= 5[10+45]
= 5×55 = 275
Hence, the sum of first ten multiple of 5 is 275.
13. If the sum of first m terms of an AP is the same as the sum of its first n terms, show that the sum of its first (m+n) terms is zero.
Solution
Let a be the first term and d be the common difference of the given AP.
Then,
Sm = Sn
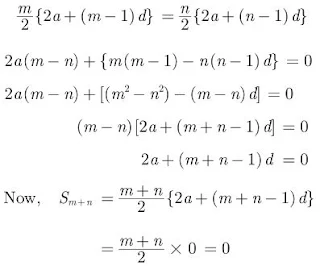


Solution
Let 1st term = a, Common difference = d
a4 = 0 a + 3d = 0
⇒ a = -3d …(i)
To prove: a25 = 3 × a11
a + 24d = 3(a + 10d) …[From (i)]
⇒ -3d + 24d = 3(-3d + 10d)
⇒ 21d = 21d
From above, a25 = 3(a11)
19. Find 10th term from end of the A.P. 4,9, 14, …, 254. (2011OD)
Solution
Common difference d = 9 – 4
= 14 – 9 = 5
Given: Last term, l = 254, n = 10
nth term from the end = l – (n – 1) d
∴ 10th term from the end = 254 – (10 – 1) × 5
= 254 – 45 = 209
20. Find, 100 is a term of the AP 25, 28, 31,.... or not.
Solution
Let the first term of an AP be a, common difference
be d and number of terms be n.
Let an = 100
Here, a = 25, d = 28-25 = 31-28 = 3
Now,
an = a + (n-1)d,
100 = 25 + (n-1) 3
⇒ 100 - 25 = 75 = (n-1) 3
⇒ 25 = n - 1
⇒ n = 26
Since, 26 is an whole number, thus 100 is a term of given A.P.
21. Find the 7th term from the end of AP 7, 10, 13,.... 184
Solution
Let us write AP in reverse order i.e., 184, .....13, 10, 7
Let the first term of an AP be a and common
difference be d.
Now,
d = 7-10 = -3
a = 184, n = 7
7th term from the original end.
a7 = a +6d
⇒ a7 = 184 + 6(-3)
= 184 -18 = 166
Hence, 166 is the 7th term from the end.
Solution
Here, an = 45, Sn = 400, a = 5, n = ?, d = ?
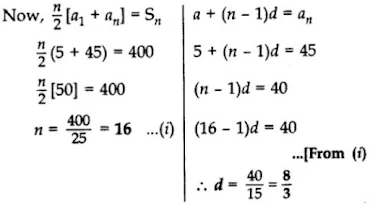
Solution
Let the first term be a, common difference be d, nth term be a n and sum of n term be Sn .
We have, a = 65, d = -5, Sn = 0

⇒ 135n - 5n2 = 0
⇒ n(135 - 5n) = 0
⇒ 5n = 135
⇒ n = 27
26. How many terms of the AP 18, 16, 14.... be taken so that their sum is zero?
Solution
Let the first term be a, common difference be d, nth term be an and sum of n term be Sn.
Here,
a = 18, d = -2, Sn = 0
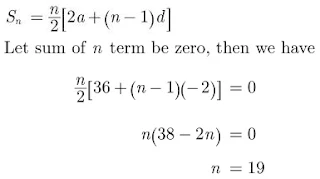

Solution
To find: 110 + 121 + 132 + … + 990
Here,
a = 110, d = 121- 110 = 11, an = 990
∴ a + (n – 1)d = 990
110 + (n – 1).11 = 990
⇒ (n – 1). 11 = 990 – 110 = 880
⇒ (n – 1) = 880 = 80
⇒ n = 80 + 1 = 81
As,
Sn = n/2 (a1 + an)
∴ S81 = 81/2 (110 + 990)
= 81/2 (1100) = 81 × 550 = 44,550
29. Find how many integers between 200 and 500 are divisible by 8.
Solution
Number divisible by 8 are 208, 2016, 224, .... 496. It is an AP
Let the first term be a, common difference be d and nth term be an.
We have a = 208, d = 8, an = 496
Now,
a + (n-1)d = an
⇒ 208 + (n-1)d = 496
⇒ (n-1)8 = 496 - 208
⇒ n = 36+1 = 37
Hence, required numbers divisible by 8 is 37.
30. The fifth term of an AP is 26 and its 10th term is 51. Find the AP
Solution
Let the first term be a, common difference be d and nth term be an.
a5 = a + 4d = 26 ...(1)
a10 = a + 9d = 51 ...(2)
Subtracting (1) from (2) we have
5d = 25
⇒ d = 5
Substituting this value of d in equation (1) we get
a = 6
Hence, the AP is 6, 11, 16, ....
32. Find whether -150 is a term of the AP 11, 8, 5, 2, ...
Solution
Let the first term be a, common difference be d and nth term be an.
Let the nth term of given AP 11, 8, 5, 2... be -150
Hence,
a = 11, d = 8-11 = -3 and an = -150
a + (n-1)d = an
⇒ 11 + (n-1)(-3) = -150
⇒ (n-1)(-3) = -161
which is not a whole number. Hence -150 is not a term of given AP.
Arithmetic Progressions Class 10 Maths Important Questions Short Answer-II (3 Marks)


Solution
Let the required term be nth term, i.e., an
Here,
d = 14 – 3 = 11, a = 3
According to the Question,
an = 99 + a25
∴ a + (n – 1) d = 99 + a + 24d
⇒ (n – 1) (11) = 99 + 24 (11)
⇒ (n – 1) (11) = 11 (9 + 24)
⇒ n – 1 = 33
⇒ n = 33 + 1 = 34
∴ 34th term is 99 more than its 25th term.
36. Which term of the AP 20, 19 1/4, 18 1/2, 17 3/4, ...is the first negative term.
Solution
Here,
a = 20

n = 28
Hence, the first negative term is 28th term.
37. If in an AP, the sum of first m terms is n and the sum of its first n terms is m, then prove that the sum of its first (m+n) terms is -(m+n)
Solution
Let 1st term of series be a and common difference be d, then we have
Sm = n
Sn = m


Solution
Given,
a19 = 3(a6)
⇒ a + 18d = 3(a + 5d)
⇒ a + 18d = 3a + 15d
⇒ 18d – 15d = 3a – a

Solution
a5 + a9 = 30 …[Given]
⇒ a + 4d + a + 8d = 30 …[∵an = a + (n – 1)d]
⇒ 2a + 12d = 30
⇒ a + 6d = 15 …[Dividing by 2]
⇒ a = 15 – 6d …(i)
Now, a52 = 3(a8)
a + 24d = 3(a + 7d)
⇒ 15 – 6d + 240 = 3(15 – 6d + 7d) …[From (i)]
⇒ 15 + 18d = 3(15 + d)
⇒ 15 + 18d = 45 + 3d
⇒ 18d – 3d = 45 – 15
⇒ 15d = 30
∴ d = 30/15 = 2
From (i), a = 15 – 6(2) = 15 – 12 = 3
42. The ninth term of an AP is equal to seven times the second term and twelfth term exceeds five times the third term by 2. Find the first term and the common difference.
Solution
Let the first term be a, common difference be d and nth term be an.
Now,
a9 = 7a2
⇒ a + 8d = 7(a+d)
⇒ a + 8d = 7a + 7d
⇒ -6a + d = 0 ...(1)
and
a12 = 5a3 + 2
⇒ a + 11d = 5(a+2d) + 2
⇒ a + 11d = 5a + 10d + 2
⇒ -4a + d = 2 ...(2)
Subtracting (2) from (1), we get
-2a = -2
⇒ a = 1
Substituting this value of a in equation (1) we get
-6 + d = 0
⇒ d = 6
Hence first term is 1 and common difference is 6.

Solution
Here 1st term, a = 18
46. If the ratio of the sums of first n terms of two AP’s is (7n + 1): (4n + 27), find the ratio of their nth terms.
Solution
Let a and A be the first term and d and D be the common difference of two AP’s, then we have

Solution
First term, a = 5, Last term, an = 45
Let the number of terms = n
Sn = 400
⇒ n/2 (a + an) = 400
⇒ n/2(5 + 45) = 400
⇒ n/2 (50) = 400
⇒ n = 400/25 = 16 = Number of terms
Now, an = 45
a + (n – 1)d = an
⇒ 5+ (16 – 1)d = 45
⇒ 15d = 45 – 5
∴ d = 40/15=8/3
48. The sum of first n terms of an AP is 3n2 + 4n. Find the 25th term of this AP.
Solution
We have, Sn = 3n2 + 4n
Put n = 25,
S25 = 3(25)2 + 4(25)
= 3(625) + 100
= 1875 + 100 = 1975
Put n = 24,
S24 = 3(24)2 + 4(24)
= 3(576) + 96
= 1728 + 96 = 1824
∴ 25th term = S25 – S24
= 1975 – 1824 = 151
49. The digits of a positive number of three digits are in A.P. and their sum is 15. The number obtained by reversing the digits is 594 less than the original number. Find the number.
Solution
Let hundred’s place digit = (a – d)
Let ten’s place digit = a
Let unit’s place digit = a + d
According to the Question,
a – d + a + a + d = 15
⇒ 3a = 15
⇒ a = 5
Original number
= 100(a – d) + 10(a) + 1(a + d)
= 100a – 100d + 10a + a + d
= 111a – 99d
Reversed number
= 1(a – d) + 10a + 100(a + d)
= a – d + 10a + 100a + 100d
= 111a + 99d
Now, Original no. – Reversed no. = 594
111a – 99d – (111a + 99d) = 594
-198d = 594
⇒ d = 594/-198 = -3
∴ The Original no. = 111a – 99d
= 111(5) – 99(-3)
= 555 + 297 = 852
50. Find the sum of all multiples of 7 lying between 500 and 900. (2012OD)
Solution
To find: 504 + 511 + 518 + … + 896
a = 504, d = 511- 504 = 7, an = 896
a + (n – 1)d = an
∴ 504 + (n – 1)7 = 896
(n – 1)7 = 896 – 504 = 392





Arithmetic Progressions Class 10 Maths Important Questions Long Answer (4 Marks)
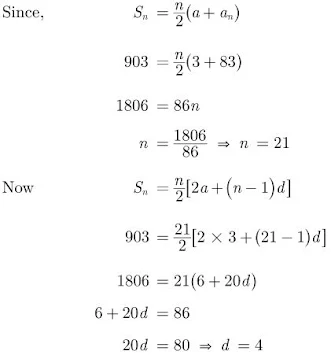

Solution
Let A be the first term and D be the common difference of the given A.P.
pth term = A + (p – 1)D = a …(i)
qth term = A + (q – 1)D = b …(ii)
rth term = A + (r – 1)D = c …(iii)
L.H.S. = (a – b)r + (b – c)p + (c – a)q
= [A + (p – 1)D – (A + (q – 1)D)]r + [A + (q – 1)D – (A + (r – 1)D)]p + [A + (r – 1)D – (A + (p – 1)D)]q
= [(p – 1 – q + 1)D]r + [(q – 1 – r + 1)D]p + [(r – 1 – p + 1)D]q
= D[(p – q)r + (q – r)p + (r – p)q]
= D[pr – qr + qp – rp + rq – pq]
= D[0] = 0 = R.H.S.
59. A sum of ₹1,600 is to be used to give ten cash prizes to students of a school for their overall academic performance. If each prize is ₹20 less than its preceding prize, find the value of each of the prizes.
Solution
Here,
S10 = 1600, d = -20, n = 10
Sn = n/2 (2a + (n – 1)d]
∴ 10/2[2a + (10 – 1)(-20)] = 1600
2a – 180 = 320
2a = 320 + 180 = 500
a = 250
∴ 1st prize = a = ₹250
2nd prize = a2 = a + d = 250 + (-20) = ₹230
3rd prize = a3 = a2 + d = 230 – 20 = ₹210
4th prize = a4 = a3 + d = 210 – 20 = ₹190
5th prize = a5 = a4 + d = 190 – 20 = ₹170
6th prize = a6 = a5 + d = 170 – 20 = ₹150
7th prize = a7 = a6 + d = 150 – 20 = ₹130
8th prize = a8 = a7 + d = 130 – 20 = ₹110
9th prize = a9 = a8 + d = 110 – 20 = ₹590
10th prize = a10 = a9 + d = 90 – 20 = ₹70
= ₹1,600
60. If the sum of first four terms of an AP is 40 and that of first 14 terms is 280. Find the sum of its first n terms.
Solution
Let a be the first term and d be the common difference.
Sum of n terms of an AP,

Hence, sum of n terms is 6n + n2.
61. If Sn denotes the sum of first n terms of an AP, prove that, S30 = 3(S20 - S10)
Solution
Let the first term be a, and common difference be d.
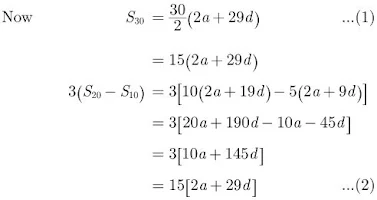
Hence, S30 = 3(S20 - S10)
62. Find the 60th term of the AP 8, 10, 12,.... if it has a total of 60 terms and hence find the sum of its last 10 terms.
Solution
Let the first term be a, common difference be d, nth term be a n and sum of n term be Sn
We have,
a = 8, d = 10 - 8 = 2
an = a + (n-1)d
Now,
a60 = 8 + (60 - 1)2
= 8+ 59×2 = 126
and a51 = 8 + 50×2
= 8 + 100 = 108
Sum of last 10 terms,

Hence sum of last 10 terms is 1170.
63. An AP consists of 37 terms. The sum of the three middle most terms is 225 and the sum of the past three terms is 429. Find the AP.
Solution
Let the middle most terms of the AP be (x-d), x and (x+d).
We have,
x-d + x + x+d = 225
⇒ 3x = 225
⇒ x = 75
and the middle term = 37+1/2 = 19th term.
Thus AP is,
(x-18d),...(x-2d), (x-d), x, (x+d), (x+2d),...(x+18d)
Sum of last three terms,
(x+18d) + (x+17d) + (x+16d) = 429
⇒ 3x + 51d = 429
⇒ 225 + 51d = 429
⇒ d = 4
First term, a1 = x-18d = 75- 18×4 = 3
a2 = 3+4 = 7
Hence, AP = 3, 7, 11,...,147.
64. The first and the last terms of an A.P. are 8 and 350 respectively. If its common difference is 9, how many terms are there and what is their sum?
Solution
Here,
a = 8, an = 350, d = 9
As we know, a + (n − 1) d = a2
∴ 8 + (n – 1) 9 = 350
⇒ (n − 1) 9 = 350 – 8 = 342
⇒ n – 1 = 342/9 = 38
⇒ n = 38 + 1 = 39
∴ There are 39 terms.
∴ Sn = n/2(a + an)
∴ S39 = 39/2 (8 + 350) = 39/2 × 358
= 39 × 179 = 6981
65. In an AP of 50 terms, the sum of first 10 terms is 210 and the sum of its last 15 terms is 2565. Find the AP.
Solution
Here,
n = 50,
S10 = 210
= 10/2 (2a + 9d) = 210 …[Sn = 1/2 [2a+(n – 1)2]
⇒ 5(2a + 9d) = 210
⇒ 2a + 9d = 210/5 = 42
⇒ 2a = 42 – 9d
⇒ a = 42−9d/2 …(i)
Now,
50 = (1 + 2 + 3 + …) + (36 + 37 + … + 50) Sum = 2565
Sum of its last 15 terms = 2565 …(Given)
S50 – S35 = 2565
⇒ 50/2(2a + 49d) – 35/2 (2a + 34d) = 2565
⇒ 100a + 2450d – 70a – 1190d = 2565 × 2
⇒ 30a + 1260d = 5130
⇒ 3a + 1260 = 513 …(Dividing both sides by 10)

Solution
Classes: 1 + I + II + … + XII
Sections: 2(I) + 2(II) + 2(III) + … + 2(XII)
Total no. of trees
= 2 + 4 + 6 … + 24
= (2 × 2) + (2 × 4) + (2 × 6) + … + (2 × 24)
= 4 + 8 + 12 + … + 48
:: S12 = 12/2(4 + 48) = 6(52) = 312 trees
67. Find the sum of first 24 terms of an AP whose nth term is given by an = 3+2n
Solution
Let the first term be a, common difference be d, nth term be an and sum of n term be Sn
We have,
an = 3+2n
a1 = 3+ 2×1 = 5
a2 = 3 + 2×2 = 7
a3 = 3 + 2×3 = 9
Thus, the series is 5, 7, 9,... in which
a = 5 and d = 2
Now,
Hence, S24 = 672
68. Ramkali required ₹500 after 12 weeks to send her daughter to school. She saved ₹100 in the first week and increased her weekly saving by ₹20 every week. Find whether she will be able to send her daughter to school after 12 weeks.
Solution
Money required by Ramkali for admission of her daughter = ₹2500
A.P. formed by saving
100, 120, 140, … upto 12 terms …(i)
Let, a, d and n be the first term, common difference and number of terms respectively.
Here,
a = 100, d = 20, n = 12
Sn = n/2 (2a + (n − 1)d)
⇒ S12 = 12/2 (2(100) + (12 – 1)20)
⇒ S12 = 12/2 [2(100) + 11(20)] = 6[420] = ₹2520
69. How many multiples of 4 lie between 10 and 250? Also find their sum. (2011D)
Solution
Multiples of 4 between 10 and 250 are:
12, 16, 20, … 248
Here, a = 12, d = 4, an = 248
As we know, a + (n – 1) d = an
∴12 + (n – 1) 4 = 248
⇒ (n – 1) 4 = 248 – 12 = 236
⇒ n – 1 = 236/4 = 59
⇒ n = 59 + 1 = 60
∴ There are 60 terms.
Now, Sn = n2 (a + an)
∴ S60 = 60/2(12 + 248)
= 30 (260) = 7800
70. The houses in a row are numbered consecutively from 1 to 49. Show that there exists a value of X such that sum of numbers of houses preceding the house numbered X is equal to sum of the numbers of houses following X.
Solution
Here,
A.P. is 1, 2, 3, …., 49
a = 1, d = 1, an = 49

Now,
⇒ (X – 1)2 (2 + (X – 2)) = 49(2 + 48) – X[2 + (x – 1)]
⇒ (X – 1). X = 2,450 – X(X + 1)
⇒ x2 – X = 2,450 – X2 – X
⇒ X2 – X + X2 + X = 2,450
⇒ 2X2 = 2,450
⇒ X2 = 1,225
∴ X = √1225 = 35 …[X can not be -ve]