NCERT Solutions for Chapter 5 Continuity and Differentiability Class 12 Maths Miscellaneous Exercise

Class 12 Maths NCERT Solutions for Chapter 5 Continuity and Differentiability Miscellaneous Exercise

Continuity and Differentiability Miscellaneous Exercise Solutions 

1. Differentiate w.r.t. x the function (3x² – 9x + 5)⁹ 

Solution

Let y =  (3x² – 9x + 5)⁹ 
Using chain rule, we obtain 
dy/dx = d/dx  (3x² - 9x + 5)⁹ 
= 9(3x² - 9x + 5)⁹ . d/dx (3x² - 9x + 5) 
= 9(3x² - 9x + 5)⁸ . (6x - 9) 
= 9(3x² - 9x + 5)⁸ . 3(2x - 3)
= 27(3x² - 9x + 5)⁸ (2x - 3)

2. Differentiate w.r.t. x the function sin³ x + cos⁶ x

Solution

Let y = sin³ x + cos⁶ x 
∴ dy/dx = d/dx (sin³ x) + d/dx (cos⁶ x) 
= 3 sin² x . d/dx (sin x) + 6 cos⁵ x . d/dx  (cos x)
= 3 sin² x . cos x + 6 cos⁵ x . (-sin x) 
= 3 sin x cosx(sin x - 2 cos⁴ x)

3. Differentiate w.r.t. x the function (5x)^{3cos 2x}

Solution

Let y =  (5x)^{3cos 2x} 
Taking logarithm on both the sides, we obtain 
log y = 3 cos 2x log 5x 
Differentiating both sides with respect to x, we obtain 

4. Differentiate w.r.t. x the function sin^-1 (x√x), 0 ≤ x ≤ 1 

Solution

Let y = sin^-1 (x√x)
Using chain rule, we obtain 

5. Differentiate w.r.t.  the function , -2 < x < 2 

Solution

6. Differentiate w.r.t. x the function 

Solution

7. Differentiate w.r.t. x the function (log x)^{log x}  , x > 1 

Solution

Let y = (log x)^{log x}  
Taking logarithm on both the sides, we obtain 
log  y = log x . log(log x) 
Differentiating both sides with respect to x, we obtain 

8. Differentiate w.r.t. x the function cos (a cos x + b sin x), for some constant a and b.

Solution

Let y = cos(a cos x + b sin x) 
By using chain rule, we obtain 
dy/dx = d/dx  cos(a cos x + b sin x) 
⇒ dy/dx = - sin(a cos x + b sin x). d/dx (a cos x + b sin x) 
= - sin (a cos x + b sin x) . [a(-sin x) + b cos x]
= (a sin x - b cos x) . sin (a cos x + bsin x) 

9. Differentiate w.r.t. x the function (sin x - cos x)^{(sin x - cos x)}  , π/4 < x < 3π/4

Solution

Let y = (sin x - cos x)^{(sin x - cos x)}  
Taking logarithm on both the sides, we obtain 
log y = log[(sin x - cos x)^{(sin x - cos x)}  ]
⇒ log y = (sin x - cos x) . log(sin x - cos x) 
Differentiating both sides with respect to x, we obtain 

where sin x > cos x 

10. Differentiate w.r.t. x the function x^x + x^a + a^x + a^a, for some fixed a > 0 and x > 0

Solution

Let y = x^x + x^a + a^x + a^a    
Also, let x^x = u, x^a = v, a^x = w, and a^a = s 
∴ y = u + v + w + s 
⇒ dy/dx = du/dx + dv/dx + dw/dx + ds/dx ...(1) 
u = x^x 
⇒ log u = log x^x 
⇒ log u = x log x 
Differentiating both sides with respect to x, we obtain 

w = a^x 
⇒ log w = log a^x 
⇒ log w = x log a 
Differentiating both sides with respect to x, we obtain 

s = a^a   
Since a is constant, a^a is also a constant. 
ds/dx = 0 ...(5) 
From (1), (2), (3), (4) and (5), we obtain 
dy/dx = x^x (1 + log x) + ax^a-1  + a^x log a + 0 
= x^x (1 + log x) + ax^a-1 + a^x log a

11. Differentiate w.r.t. x the function x^x2-3 + (x - 3)^x2, for x > 3 

Solution 

Let y = x^x2-3  + (x - 3)^x2         
Also, let u = x^x2-3 and v = (x - 3)^x2  
∴ y = u + v 
Differentiating both sides with respect to x, we obtain 
dy/dx = du/dx + dv/dx ...(1) 
u = x^x2-3  
∴ log u = log(x^x2-3)
log u = (x² - 3) log x
Differentiating with respect to x, we obtain 

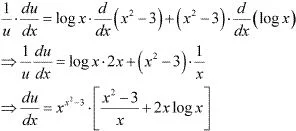
Also, 
v =(x - 3)^x2  
∴ log v = log (x - 3)^x2  
⇒ log v = x² log (x - 3) 
Differentiating both sides with respect to x, we obtain 

12. Find dy/dx , if y = 12(1 - cos t), x = 10(t - sin t), - π/2 < t < π/2

Solution

It is given that, y = 12 (1 - cost), x = 10(t - sin t) 

13. Find dy/dx , if y = sin^-1 x + sin^-1 √(1 - x² ), 0 < x < 1 

Solution

14. If x√(1 + y) + y√(1 + x) = 0, for, -1<x<1, prove that dy/dx = 1/(1 + x)² 

Solution

It is given that, 
x√(1 + y) + y√(1 + x) = 0
⇒ x√(1 + y)  = - y√(1 + x)
Squaring both sides, we obtain 
x² (1 + y) = y² (1 + x)
⇒ x² + x² y = y² + xy² 
⇒ x² - y² = xy² - x² y
⇒ x² - y² = xy(y - x)
⇒ (x + y)(x - y) = xy(y - x)
∴ x + y = -xy
⇒ (1 + x)y = -x 
⇒ y = -x/(1 + x) 
Differentiating both sides with respect to x, we obtain 
y = -x/(1 + x) 

15. If (x – a)² + (y – b)² = c², for some c > 0, prove that  is a constant independent of a and b. 

Solution

Differentiating both sides with respect to x, we obtain 

Hence, proved. 

16. If cos y = x cos (a + y), with cos a ≠ ± 1, prove that dy/dx = [cos² (a + y)]/ sin a 

Solution

It is given that, cos y = x cos(a + y) 
∴ d/dx [ cos y] = d/dx [x cos(a + y)] 

17. If x = a (cos t + t sin t) and y = a (sin t – t cos t), find d² y/dx²  . 

Solution

It is given that, x = a(cost + t sin t) and y = a(sin t - t cos t) 
∴ dx/dt = a . d/dt (cos t + t sin t) 

18. If f (x) = |x|³, show that f ″(x) exists for all real x and find it.

Solution

It is known that, |x| = 
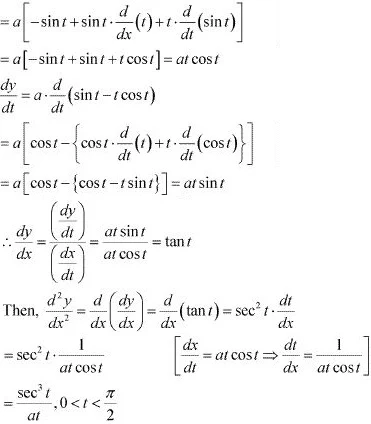
Therefore, when x ≥ 0, f(x) = |x|³ = x³ 
In this case, f '(x) = 3x² and hence, f ''(x) = 6x 
When x < 0, f(x) = |x|³ = (-x)³ = -x³ 
In this case, f '(x) = -3x² and hence, f ''(x) = -6x 
Thus, for f(x) = |x|³ , f ''(x) exists for all real x and is given by, 
f ''(x) 

19. Using mathematical induction prove that d/dx (xⁿ ) = nx^n-1 for all positive integers n. 

Solution

To prove : p(n) : d/dx (xⁿ ) = nx^n-1 for all positive integers n 
for n = 1, 
p(1) : d/dx (x) = 1 = 1 .x^1-1 
P(n) is true for n = 1 
Let P(k) is true for some positive integer k. 
That is, P(k) : d/dx (x⁴ ) = kx^k-1 
It has to be proved that P(k + 1) is also true. 

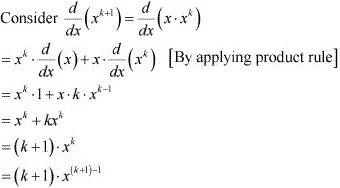
Thus, P(k + 1) is true whenever P (k) is true. 
Therefore, by the principle of mathematical induction, the statement P (n) is true for every positive integer n. 
Hence, proved. 

20. Using the fact that sin (A + B) = sin A cos B + cos A sin B and the differentiation, obtain the sum formula for cosines

Solution

sin (A + B) = sin A cos B + cos A sin B
Differentiating both sides with respect to x, we obtain 

21. Does there exist a function which is continuous everywhere but not differentiable at exactly two points? Justify your answer ?

Solution

Yes, 
Consider the function f(x) = |x - 1| + |x - 2|
Since we know that the modulus function is continuous everywhere, so there sum is also continuous. 
Therefore, function f is continuous everywhere 
Now, let us check the differentiability of f(x) at x = 1, 2 
At x = 1 

Therefore, f is not differentiable at x = 1. 
At x = 2 

= -0 
Now,  

 = 2 
≠ LHD 
Therefore, f is not differentiable at x = 2. 
Hence, f is not differentiable at exactly two points. 

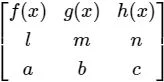22. If y =, prove that 

Solution 

23. If y = e^{a cos-1  x}   , -1 < = x < 1 show that (1 - x² ) d² y/dx²  - x . dy/dx  - a² y = 0 

Solution