Class 12 Maths NCERT Solutions for Chapter 5 Continuity and Differentiability Miscellaneous Exercise

Continuity and Differentiability Miscellaneous Exercise Solutions
1. Differentiate w.r.t. x the function (3x2 – 9x + 5)9
Solution
Let y = (3x2 – 9x + 5)9
Using chain rule, we obtain
dy/dx = d/dx (3x2 - 9x + 5)9
= 9(3x2 - 9x + 5)9 . d/dx (3x2 - 9x + 5)
= 9(3x2 - 9x + 5)8 . (6x - 9)
= 9(3x2 - 9x + 5)8 . 3(2x - 3)
= 27(3x2 - 9x + 5)8 (2x - 3)
2. Differentiate w.r.t. x the function sin3 x + cos6 x
Solution
Let y = sin3 x + cos6 x
∴ dy/dx = d/dx (sin3 x) + d/dx (cos6 x)
= 3 sin2 x . d/dx (sin x) + 6 cos5 x . d/dx (cos x)
= 3 sin2 x . cos x + 6 cos5 x . (-sin x)
= 3 sin x cosx(sin x - 2 cos4 x)
3. Differentiate w.r.t. x the function (5x)3cos 2x
Solution
Let y = (5x)3cos 2x
Taking logarithm on both the sides, we obtain
log y = 3 cos 2x log 5x
Differentiating both sides with respect to x, we obtain
4. Differentiate w.r.t. x the function sin-1 (x√x), 0 ≤ x ≤ 1
Solution
Let y = sin-1 (x√x)
Using chain rule, we obtain
5. Differentiate w.r.t. the function 
Solution



Taking logarithm on both the sides, we obtain
log y = log x . log(log x)
Differentiating both sides with respect to x, we obtain

By using chain rule, we obtain
dy/dx = d/dx cos(a cos x + b sin x)
⇒ dy/dx = - sin(a cos x + b sin x). d/dx (a cos x + b sin x)
= - sin (a cos x + b sin x) . [a(-sin x) + b cos x]
= (a sin x - b cos x) . sin (a cos x + bsin x)
Taking logarithm on both the sides, we obtain
log y = log[(sin x - cos x)(sin x - cos x) ]
⇒ log y = (sin x - cos x) . log(sin x - cos x)
Differentiating both sides with respect to x, we obtain

where sin x > cos x
Also, let xx = u, xa = v, ax = w, and aa = s
∴ y = u + v + w + s
⇒ dy/dx = du/dx + dv/dx + dw/dx + ds/dx ...(1)
u = xx
⇒ log u = log xx
⇒ log u = x log x
Differentiating both sides with respect to x, we obtain

⇒ log w = log ax
⇒ log w = x log a
Differentiating both sides with respect to x, we obtain

s = aa
Since a is constant, aa is also a constant.
ds/dx = 0 ...(5)
From (1), (2), (3), (4) and (5), we obtain
dy/dx = xx (1 + log x) + axa-1 + ax log a + 0
= xx (1 + log x) + axa-1 + ax log a
Also, let u = xx2-3 and v = (x - 3)x2
∴ y = u + v
Differentiating both sides with respect to x, we obtain
dy/dx = du/dx + dv/dx ...(1)
u = xx2-3
∴ log u = log(xx2-3)
log u = (x2 - 3) log x
Differentiating with respect to x, we obtain
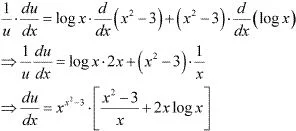
Also,
v =(x - 3)x2
∴ log v = log (x - 3)x2
⇒ log v = x2 log (x - 3)
Differentiating both sides with respect to x, we obtain



x√(1 + y) + y√(1 + x) = 0
⇒ x√(1 + y) = - y√(1 + x)
Squaring both sides, we obtain
x2 (1 + y) = y2 (1 + x)
⇒ x2 + x2 y = y2 + xy2
⇒ x2 - y2 = xy2 - x2 y
⇒ x2 - y2 = xy(y - x)
⇒ (x + y)(x - y) = xy(y - x)
∴ x + y = -xy
⇒ (1 + x)y = -x
⇒ y = -x/(1 + x)
Differentiating both sides with respect to x, we obtain
y = -x/(1 + x)

 is a constant independent of a and b.
is a constant independent of a and b. 
Hence, proved.
∴ d/dx [ cos y] = d/dx [x cos(a + y)]

∴ dx/dt = a . d/dt (cos t + t sin t)
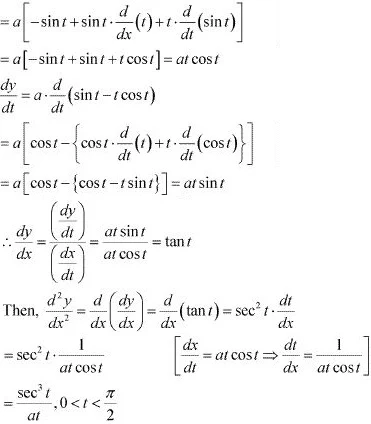
Therefore, when x ≥ 0, f(x) = |x|3 = x3
In this case, f '(x) = 3x2 and hence, f ''(x) = 6x
When x < 0, f(x) = |x|3 = (-x)3 = -x3
In this case, f '(x) = -3x2 and hence, f ''(x) = -6x
Thus, for f(x) = |x|3 , f ''(x) exists for all real x and is given by,
f ''(x)
for n = 1,
p(1) : d/dx (x) = 1 = 1 .x1-1
P(n) is true for n = 1
Let P(k) is true for some positive integer k.
That is, P(k) : d/dx (x4 ) = kxk-1
It has to be proved that P(k + 1) is also true.
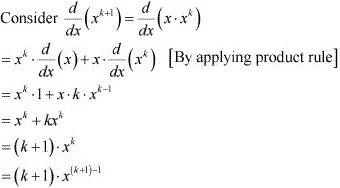
Thus, P(k + 1) is true whenever P (k) is true.
Therefore, by the principle of mathematical induction, the statement P (n) is true for every positive integer n.
Hence, proved.
Differentiating both sides with respect to x, we obtain

Consider the function f(x) = |x - 1| + |x - 2|
Since we know that the modulus function is continuous everywhere, so there sum is also continuous.
Therefore, function f is continuous everywhere
Now, let us check the differentiability of f(x) at x = 1, 2
At x = 1

At x = 2

= -0
Now,

= 2
≠ LHD
Therefore, f is not differentiable at x = 2.
Hence, f is not differentiable at exactly two points.
 , prove that
, prove that 




