Class 12 Maths NCERT Solutions for Chapter 6 Application of Derivatives Exercise 6.2

Application of Derivatives Exercise 6.2 Solutions
1. Show that the function given by f(x) = 3x + 17 is strictly increasing on R.
Solution
Let x1 and x2 be any two numbers in R.
Then, we have :
x1 < x2
⇒ 3x1 < 3x2
⇒ 3x1 + 17 < 3x2 + 17
⇒ f(x1) < f(x2)
Hence, f is strictly increasing on R.
Alternate method :
f '(x) = 3 > 0, in every interval or R.
Thus, the function is strictly increasing on R.
2. Show that the function given by f(x) = 3x + 17 is strictly increasing on R.
Solution
Let x1 and x2 be any two numbers in R.
Then, we have :
x1 < x2
⇒ 2x1 < 2x2
⇒ e2x1 < e2x2
⇒ f(x1) < f (x2)
Hence, f is strictly increasing on R.
3. Show that the function given by f(x) = sin x is
(a) strictly increasing in (0,π/2)
(b) strictly decreasing in (π/2,π)
(c) neither increasing nor decreasing in (0, π)
Solution
The given function is f(x) = sin x.
∴ f '(x) = cos x
(a) Since for each x ∊ (0, π/2), cos x > 0, we have f '(x) > 0 .
Hence, f is strictly increasing in (0, π/2).
(b) Since for each x ∊ (π/2, π), cos x < 0, we have f '(x) < 0.
Hence, f is strictly decreasing in (π/2, π).
(c) From the results obtained in (a) and (b) , it is clear that f is neither increasing nor decreasing in (0, π).
4. Find the intervals in which the function f given by f(x) = 2x2 − 3x is
(a) strictly increasing
(b) strictly decreasing
Solution
The given function is f(x) = 2x2 - 3x .
f '(x) = 4x - 3
∴ f '(x) = 0
⇒ x = 3/4
Now, the point 3/4 divides the real line into two disjoint intervals i.e., ( - ∞, 3/4) and (3/4, ∞).

Hence, the given function (f) is strictly decreasing in interval (- ∞, 3/4).
In interval (3/4, ∞), f '(x) = 4x - 3 > 0.
Hence, the given function (f) is strictly increasing in interval (3/4 , ∞).
(a) strictly increasing
(b) strictly decreasing
f '(x) = 6x2 - 6x - 36 = 6(x2 - x - 6) = 6(x + 2)(x - 3)
∴ f '(x) = 0 ⇒ x = -2, 3
The points x = -2 and x = 3 divide the real line into three disjoint intervals i.e.,
(- ∞, -2), (-2, 3), and (3, ∞).
Hence, the given function (f) is strictly increasing in intervals (-∞, -2) and (3, ∞), while function (f) is strictly decreasing in interval (-2, 3).
(a) x2 + 2x − 5
(b) 10 − 6x − 2x2
(c) -2x3 - 9x2 - 12x + 1
(d) 6 - 9x - x2
(e) (x + 1)3 (x - 3)3
f(x) = x2 + 2x - 5
∴ f '(x) = 2x + 2
Now,
f '(x) = 0
Point x = -1 divides the real line into two disjoint intervals i.e., (- ∞, -1) and (-1, ∞) .
In interval (- ∞, -1), f '(x) = 2x + 2 < 0.
∴ f is strictly decreasing in interval ( -∞. -1).
Thus, f is strictly decreasing for x < - 1.
In interval (-1, ∞), f '(x) = 2x + 2 > 0.
∴ f is strictly increasing in interval (-1, ∞).
Thus, f is strictly increasing for x > -1.
f(x) = 10 - 6x - 2x2
∴ f'(x) = -6 - 4x
Now,
f '(x) = 0
The point x = -3//2 divides the real line into two disjoint intervals i.e., (-∞, -3/2) and (-3/2, ∞).
In interval (-∞, -3/2) i.e., when x < -3/2, f '(x) = -6 - 4x > 0.
∴ f is strictly increasing for x < -3/2.
In interval (-3/2, ∞) i.e., when x > -3/2, f '(x) = -6 - 4x < 0.
∴ f is strictly decreasing for x > -3/2.
f(x) = -2x3 - 9x2 - 12x + 1
∴ f '(x) = -6x2 - 18x - 12 = -6(x2 + 3x + 2) = -6(x + 1)(x + 2)
Now,
f '(x) = 0
Points x = -1 and x = -2 divide the real line into three disjoint intervals
i.e., (-∞, -2), (-2, -1), and (-1, ∞).
In intervals (-∞, -2) and (-1, ∞)i.e., when x < -2 and x > -1,
f '(x) = -6(x + 1)(x + 2) < 0
∴ f is strictly decreasing for x < -2 and x > -1.
Now, in interval (-2, -1) i.e., when -2 < x < - 1, f '(x) = -6(x + 1)(x + 2) > .
∴ f is strictly increasing for -2 < x < -1.
f(x) = 6 - 9x - x2
∴ f '(x) = -9 - 2x
Now, f '(x) = 0 gives x = -9/2
The point x = -9/2 divides the real line into two disjoint intervals i.e., (-∞, -9/2) and (-9/2, ∞).
In interval (-∞, -9/2) i.e., for x < -9/2, f '(x) = -9 - 2x > 0.
∴ f is strictly increasing for x < -9/2.
∴ f is strictly decreasing for x > -9/2.
f(x) = (x + 1)3 (x - 3)3
f '(x) = 3(x + 1)3 (x - 3)3 + 3(x - 3)2 (x + 1)3
= 3(x + 1)2 (x - 3)2 [x - 3 + x + 1]
=3(x + 1)2 (x - 3)2 (2x - 2)
= 6(x + 1)2 (x - 3)2 (x - 1)
Now,
f '(x) = 0
The points x = -1, x = 1, and x = 3 divide the real line into four disjoint intervals i.e., (-∞, -1), (-1, 1), (1, 3), and (3, ∞) .
In intervals (-∞, -1) and (-1, 1), f '(x) = 6(x + 1)2 (x - 3)2 (x - 1) < 0.

Hence, f is a increasing function throughout its domain.
y = [x(x - 2)]2 = [x2 - 2x]2
∴ dy/dx = y' = 2(x2 - 2x)(2x - 2) = 4x(x - 2)(x - 1)
∴ dy/dx = 0 ⇒ x = 0, x = 2, x = 1.
The points x = 0, x = 1, and x = 2 divide the real line into four disjoint intervals
i.e., (- ∞, 0), (0, 1)(1, 2), and (2, ∞).
In intervals ( - ∞, 0) and (1, 2), dy/dx < 0.
∴ y is strictly decreasing in intervals (- ∞, 0) and (1, 2).
However, in intervals (0, 1) and (2, ∞), dy/dx > 0.
∴ y is strictly increasing for 0 < x < 1 and x > 2.
y = 4 sinθ/(2 + cos θ) - θ

⇒ cos2 θ - 4cos θ = 0
⇒ cos θ (cos θ - 4) = 0
⇒ cos θ = 0 or cos θ = 4
Since cos θ ≠ 4, cos θ = 0.
cos θ = 0
Now,
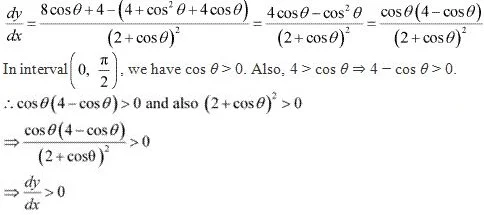
Also, the given function is continuous at x = 0 and x = π/2
Hence, y is increasing in interval [0, π/2).
∴ f '(x) = 1/x
It is clear that for x > 0, f '(x) = 1/x >0.
Hence, f(x) = log x is strictly increasing in interval (0, ∞)
Now, f '(x) = 0 ⇒ x = 1/2.
The point 1/2 divides the interval (-1, 1) into two disjoint intervals i.e., (-1, 1/2) and (1/2, 1).
Now, in interval (-1, 1/2), f '(x) = 2x - 1 < 0.
Therefore, f is strictly decreasing in interval (-1, 1/2).
However, in interval (1/2 , 1), f '(x) = 2x - 1 > 0.
Therefore, f is strictly increasing in interval (1/2, 1).
Hence, f is neither strictly increasing nor decreasing in interval (-1, 1).
(A) cos x
(B) cos 2x
(C) cos 3x
(D) tan x
∴ f '1 (x) = - sin x
In interval (0, π/2), f '1 (x) = - sin x < 0.
∴ f '2 (x) = - 2sin 2x
Now, 0 < x < π/2
∴ f '2 (x) = - 2sin 2x < 0 on (0, π/2)
∴ f2 (x) = cos 2x is strictly decreasing in interval (0, π/2).
f’3 (x) = -3 sin 3x
Now, f’3 (x) = 0.
⇒ sin 3x = 0
⇒ x = π/3
The point x = π/3 divides the interval (0, π/2) into two disjoint intervals
i.e., 0(0, π/3) and (π/3, π/2).
Now, in interval (0, π/3), f3 (x) = -3 sin 3x > 0 [as π/3 < x < π/2 ⇒ π < 3x < 3π/2].
∴ f3 is strictly increasing in interval (π/3 , π/2) .
Hence, f3 is neither increasing nor decreasing in interval (0, π/2).
∴ f’4 (x) = sec2 x
In interval (0, π/2), f’4 (x) = sec2 x > 0.
∴ f4 is strictly increasing in interval (0, π/2).
Therefore, functions cos x and cos 2x are strictly decreasing in (0, π/2).
Hence, the correct answer are A and B.
(A) (0,1)
(B) (π/2,π)
(C) (0,π/2)
(D) None of these
f(x) = x100 + sin x –1
∴ f '(x) = 100x99 + cos x
In interval (0, 1), cos x > 0 and 100x99 > 0.
∴ f '(x) > 0.
Thus, function f is strictly increasing in interval (0, 1).
∴ f '(x) > 0 in (π/2 , π)
Thus, function f is strictly increasing in interval (π/2 , π).
In interval (0 , π/2), cos x > 0 and 100x99 > 0.
∴ 100x99 + cos x > 0
⇒ f '(x) > 0 on (0, π/2)
∴ f is strictly increasing in interval (0, π/2).
Hence, function f is strictly decreasing in none of the intervals.
The correct answer is D.
f(x) = x2 + ax + 1
∴ f '(x) = 2x + a
Now, function f will be increasing in (1, 2), if f '(x) > 0 in (1, 2).
f '(x) > 0
⇒ 2x + a > 0
⇒ 2x > - a
⇒ x > -a/2
Therefore, we have to find the least value of a such that
x > -a/2, when x ∊(1, 2).
⇒ x > -a/2 (when 1 < x < 2)
Thus, the least value of a for f to be increasing on (1, 2) is given by,
-a/2 = 1
-a/2 = 1
Hence, the required value of a is -2.
f(x) = x + 1/x
∴ f '(x) = 1 - 1/x2
Now,
f '(x) = 0 ⇒ 1/x2 = 1 ⇒ x = ± 1
The points x = 1 and x = -1 divide the real line in three disjoint intervals
i.e., (-∞, -1), (-1, 1) and (1, ∞).
In interval (-1, 1), it is observed that :
⇒ x2 < 1
⇒ 1 < 1/x2 , x ≠ 0
⇒ 1 - 1/x2 < 0, x ≠ 0
∴ f '(x) = 1 - 1/x2 < 0 on (-1, 1) ~ {0}.
∴ f is strictly decreasing on (-1, 1) ~ {0}.
In intervals (- ∞, -1) and (1, ∞), it is observed that :
x < -1 or 1 < x
⇒ x2 > 1
⇒ 1 > 1/x2
⇒ x - 1/x2 > 0
∴ f '(x) = 1 - 1/x2 > 0 on (-∞, 1) and (1, ∞).
∴ f is strictly increasing on (- ∞, 1) and (1, ∞).
Hence, function f is strictly increasing in interval I disjoint from (-1, 1).
Hence, the given result is proved.
f(x) = log sin x
∴ f '(x) = (1/sin x) cos x = cot x
In interval (0, π/2), f '(x) = cot x > 0.
∴ f is strictly increasing in (0, π/2).
In interval (π/2, π) , f '(x) = cos x < 0.
∴ f is strictly decreasing in (π/2 , π).
f(x) = log cosx

f(x) = x3 - 3x2 + 3x - 100
f '(x) = 3x2 - 6x + 3
= 3(x2 - 2x + 1)
= 3(x - 1)2
For any x ∈ R, (x - 1)2 > 0.
Thus, f '(x) is always positive in R.
Hence, the given function (f) is increasing in R.
(A) (– ∞, ∞)
(B) (– 2, 0)
(C) (2, ∞)
(D) (0, 2)
y = x2 e–x
Now, dy/dx = 0.
⇒ x = 0 and x = 2
The points x = 0 and x = 2 divide the real line into three disjoint intervals
i.e., (-∞, 0), (0, 2), and (2, ∞).
In intervals (-∞, 0) and (2, ∞), f '(x) < 0 as e–x is always positive.
∴ f is decreasing on (- ∞, 0) and (2, ∞).
In interval (0, 2), f '(x) > 0.
∴ f is strictly increasing on (0, 2).
Hence, f is strictly increasing in interval (0, 2).

