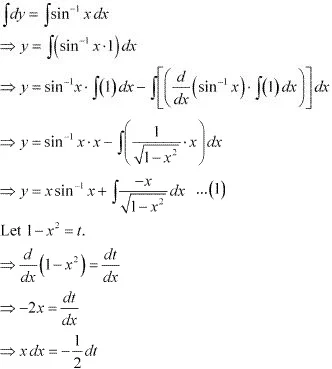NCERT Solutions for Chapter 9 Differential Equations Class 12 Maths Exercise 9.4

Class 12 Maths NCERT Solutions for Chapter 9 Differential Equations Exercise 9.4

Differential Equations Exercise 9.4 Solutions

1. For the differential equations find the general solution :  
dy/dx = (1 - cos x)/(1 + cos x) 

Solution

The given differential equation is :  

Separating the variables, we get :  

Now, integrating both sides of this equation, we get : 

⇒ y = 2 tan(x/2) - x + C
This is the required general solution of the given differential equation.

2. For the differential equation find the general solution : 
dy/dx = √(4 – y²) (-2 < y < 2) 

Solution

The given differential equation is : 
dy/dx = √(4 – y²) 
Separating the variables, we get :  
⇒ dy/√(4 – y²)  = dx 
Now, integrating both sides of this equation, we get :  

⇒ y/2 = sin(x + C) 
⇒ y = 2 sin (x + C) 
This is the required general solution of the given differential equation.

3. For the differential equations find the general solution : 
dy/dx + y = 1(y ≠ 1) 

Solution

The given differential equation is : 
dy/dx + y = 1 
⇒ dy + y dx = dx 
⇒ dy = (1 - y) dx
Separating the variables, we get : 
⇒ dy/(1 - y) = dx 
Now, integrating both sides, we get : 

⇒ -log(1 - y) = x + log C 
⇒ - log C - log (1 - y) = x 
⇒ log C(1 - y) = -x 
⇒ C(1 - y) = e^-x 

⇒ y = 1 + Ae^-x (where A = -1/C) 
This is the required general solution of the given differential equation.

4. For the differential equations find the general solution:
sec² x tan y dx + sec² y tan x dy = 0

Solution

The given differential equation is : 
sec² x tan y dx + sec² y tan x dy = 0  

⇒ sec² x = dt/dx
⇒ sec² x dx = dt  

= log t 
= log (tan x) 
Similarly, 
Substituting these values in equation (1), we get :  
log (tan x) = - log (tan y) + log C 
⇒ log (tan x) = log (C/tan y) 
⇒ tan x = C/tan y 
⇒ tan x tan y = C 
This is the required general solution of the given differential equation.

5. For the differential equations find the general solution:
(e^x + e^–x) dy – (e^x – e–x) dx = 0

Solution

The given differential equation is :
(e^x + e^–x) dy – (e^x – e^-x ) dx = 0
⇒ (e^x + e^-x ) dy = (e^x - e^-x )dx 

Let (e^x + e^–x) = t 
Differentiating both sides with respect to x, we get : 

⇒ (e^x + e^–x) dx = dt 
Substituting his value in equation (1), we get : 
y = ∫(1 + t) dt  + C
⇒ y = log(t) + C 
⇒ y = log (e^x + e^–x) + C
This is the required general solution of the given differential equation.

6. For the differential equations find the general solution: 
dy/dx = (1 + x² )(1+ y²) 

Solution

The given differential equation is :  
dy/dx = (1 + x² )(1+ y²)  
⇒ dy/(1 + y² ) = (1 + x²)dx 
Integrating both sides of this equation, we get :  

⇒ tan^-1 y = ∫dx + ∫x² dx 
⇒ tan^-1 y = x + x³/3 + C 
This is the required general solution of the given differential equation.

7. For the differential equations find the general solution :  
y log y dx - x dy = 0 

Solution

The given differential equation is : 
y log y dx - x dy = 0 
⇒ y log y dx = x dy 
⇒ dy/(y log y) = dx/ x  
Integrating both sides, we get : 
∫dy/(y log y) = ∫ dx/x  ...(1)
Let log y = t 

Substituting this value in equation (1), we get :  
 ∫dt/t =  ∫dx/x 
⇒ log t = log x + log C
⇒ log (log y) = log Cx
⇒ log y = Cx
⇒ y = e^cx
This is the required general solution of the given differential equation.

8. For the differential equations find the general solution :  
x⁵ (dy/dx) = -y⁵ 

Solution

The given differential equation is :  

Integrating both sides, we get :  

⇒ x^-4 + y^-4 = -4k 
⇒ x^-4 + y^-4 = C (C = -4k) 
This is the required general solution of the given differential equation.

9. For the differential equation find the general solution : 
e^x tan y dx + (1 – e^x) sec² y dy = 0 

Solution

The given differential equation is : 
dy/dx = sin^-1 x 
⇒ dy = sin^-1 x dx 
Integrating both sides, we get : 

Substituting this value in equation (1), we get : 

⇒ y = x sin^-1 x + √t + C 
⇒ y = x sin^-1 x + √(1 - x²) + C
This is the required general solution of the given differential equation.

10. For the differential equations find the general solution:
e^x tan y dx + (1 – e^x) sec² y dy = 0 

Solution

The given differential equation is :  
e^x tan y dx + (1 – e^x) sec² y dy = 0 
(1 - e^x )sec² y dy = -e^x tan y dx 
Separating the variables, we get : 

Now, let 1 - e^x = t.
∴ d/dx (1 - e^x) = dt/dx 
⇒ -e^x = dt/dx 
⇒ -e^x dx = dt 

⇒ log (tan y) = log (1 - e^x ) + log C 
⇒ log (tan y) = log [C(1 - e^x )] 
⇒ tan y = C(1 - e^x )
This is the required general solution of the given differential equation.

11. For each of the differential equations find a particular solution satisfying the given condition:
(x³ + x² + x + 1) dy/dx = 2x² + x; y = 1 when x = 0

Solution

The given differential equation is :  

⇒ 2x² + x = Ax² + A + Bx² + Bx + Cx + C 
⇒ 2x² + x = (A + B)x² + (B + C)x + (A + C) 
Comparing the coefficients of x² and x, we get : 

A +  B = 2
B + C = 1
A + C = 0
Solving these equations, we get :  
A = 1/2, B = 3/2 and C = -1/2 
Substituting the values of A, B and C in equation (2), we get :  

Now, y = 1 when x = 0. 
⇒ 1 = (1/4) log (1) - (1/2) tan^-1 0 + C 
⇒ 1 = (1/4) × 0 - (1/2) × 0 + C 
⇒ C = 1 
Substituting C = 1 in equation (3), we get : 
y = [(1/4) log (x + 1)² (x² + 1)³] - (1/2) tan^-1 x + 1

12. For each of the differential equations find a particular solution satisfying the given condition : 
x(x² - 1) dy/dx = 1, y = 0 when x = 2 

Solution

x(x² - 1) dy/dx = 1

Comparing the coefficients of x², x and constant, we get : 
A = -1
B - C = 0
A + B + C = 0
Solving these equations, we get B = 1/2 and C = 1/2 . 
Substituting the values of A, B, and C in equation (2), we get :  

⇒ 3k²/4 = 1
⇒ 3k² = 4 
⇒ k² = 4/3 
Substituting the value of k² in equation (3), we get : 

13. For each of the differential equations find a particular solution satisfying the given condition:
cos (dx/dy) = a (a ∈ R); y = 1 when x = 0 

Solution

cos (dy/dx) = a 
⇒ dy/dx = cos^-1 a 
⇒ dy = cos^-1 a dx 
Integrating both sides, we get : 
∫dy = cos^-1 a ∫dx 
⇒ y = cos^-1 a . x + C 
⇒ y = x cos^-1 a + C  ...(1) 
Now, y = 1 when x = 0 
⇒ 1 = 0. cos^-1 a + C 
⇒ C = 1 
Substituting C = 1 in equation (1), we get :  
y = x cos^-1 a + 1 
⇒ (y -1)/x = cos^-1 a  
⇒ cos[(y -1)/x] = a 

14. For each of the differential equations find a particular solution satisfying the given condition:
dy/dx = y tan x; y = 1 when x = 0

Solution 

dy/dx = y tan x 
⇒ dy/y = tan x dx 
Integrating both sides, we get :  
∫dy/y = ∫tan x dx 

⇒ log y = log(sec x) + log C 
⇒ log y = log (C sec x) 
⇒ y = C sec x  ...(1) 

Now, y = 1 when x = 0. 
⇒1 = C × sec 0 
⇒1 = C × 1
⇒ C = 1 
Substituting C = 1 in equation (1), we get :  
y = sec x 

15. Find the equation of a curve passing through the point (0, 0) and whose differential equation is y′ = e^x sin x.

Solution

The differential equation of the curve is :  

y' = e^x sin x
⇒ dy/dx = e^x sin x
⇒ dy = e^x sin x dx 
Integrating both sides, we get :  
∫dy = ∫e^x sin x dx ...(1) 
Let I = ∫e^x sin x dx. 

⇒ I = e^x sin x - e^x sin x - I 
⇒ 2I = e^x (sin x - cos x) 
⇒ I = [e^x (sin x - cos x)]/2 

Substituting this value in equation (1), we get : 
y = [e^x (sin x - cos x)]/2 + C ...(2) 
Now, the curve passes through point (0, 0) 

⇒ 2y = e^x (sin x - cos x) + 1 
⇒ 2y - 1 = e^x (sin x - cos x) 
Hence, the required equation of the curve is 2y - 1 = e^x (sin x - cos x).

16. For the differential equation xy (dy/dx) = (x + 2)(y + 2) find the solution curve passing through the point (1, -1).

Solution

The differential equation of the given curve is :  

⇒ y - 2log(y + 2) = x + 2log x + C 
⇒ y - x - C = log x² + log (y + 2)² 
⇒ y - x - C = log [x² (y + 2)² ]  ...(1) 
Now, the curve passes through point (1, -1). 
⇒ -1 - 1 - C = log[(1)² (-1 + 2)² ] 
⇒ -2 - C = log  1 = 0 
⇒ C = -2
Substituting C = -2 in equation (1), we get :  
y - x + 2 = log[x² (y + 2)² ]
This is the required solution of the given curve.

17. Find the equation of a curve passing through the point (0, –2) given that at any point (x ,y) on the curve, the product of the slope of its tangent and y-coordinate of the point is equal to the x-coordinate of the point.

Solution

Let x and y be the x - coordinate and y - coordinate of the point on the curve respectively. 
We know that the slope of a tangent to the curve in the coordinate axes is given by the relation. 
dy/dx 
According to the given information, we get :  
y (dy/dx) = x 
⇒y dy = x dx  
Integrating both sides, we get:  
∫y dy = ∫x dx 
⇒ y²/2 = x² /2 + C 
⇒ y² - x² = 2C ...(1) 
Now, the curve passes through point (0, -2). 
∴ (-2)² - 2² = 2C 
⇒ 2C = 4 
Substituting 2C = 4 in equation (1), we get : 
y² - x² = 4 
This is the required equation of the curve.

18. At any point (x, y) of a curve, the slope of the tangent is twice the slope of the line segment joining the point of contact to the point (– 4, –3). Find the equation of the curve given that it passes through (–2, 1).

Solution

It is given that (x, y) is the point of contact of the curve and its tangent. 

The slope (m₁ ) of the line segment joining (x, y) and (-4, -3) is (y +3)/(x + 4) 
We know that the slope of the tangent to the curve is given by the relation, 
dy/dx 
∴ Slope (m₂ ) of the tangent = dy/dx 
According to the given information :  
m₂ = 2m₁ 

⇒ log (y + 3) = 2 log (x + 4) + log C 
⇒ log (y + 3) = log C (x + 4)² 
⇒ y + 3 = C(x + 4)² ...(1) 
This is the general equation of the curve. 
It is given that it passes through point (-2, 1). 
⇒ 1 + 3 = C(-2 + 4)²   
⇒ 4 = 4C 
⇒ C = 1 
Substituting C = 1 in equation (1), we get : 
y + 3 = (x + 4)²  
This is the required equation of the curve. 

19. The volume of spherical balloon being inflated changes at a constant rate. If initially its radius is 3 units and after 3 seconds it is 6 units. Find the radius of balloon after t seconds.

Solution

Let the rate of change of the volume of the balloon be k (where k is a constant ) 

⇒ 4πr³ = 3(kt + C)  ...(1) 
Now, at  t = 0, r = 3,
⇒ 4π × 3³ = 3 (k × 0 + C)
⇒ 108π = 3C
⇒ C = 36π
At t = 3, r = 6:
⇒ 4π × 6³ = 3 (k × 3 + C)
⇒ 864π = 3 (3k + 36π)
⇒ 3k = –288π – 36π = 252π
⇒ k = 84π
Substituting the values of k and C in equation (1), we get: 
4πr³ = 3(84πt + 36π)
⇒ 4πr³ = 4π(63t + 27)
⇒ r³ = 63t + 27 
⇒ r = (63t + 27)^1/3 
Thus, the radius of the balloon after t seconds is (63t + 27)^1/3 . 

20. In a bank, principal increases continuously at the rate of r% per year. Find the value of r if Rs 100 doubles itself in 10 years (log­_e2 = 0.6931).

Solution

Let p, t,  and r represent the principal, time, and rate of interest respectively. 
It is given that the principal increases continuously at the rate of r% per year. 

It is given that when t = 0, p = 100. 
⇒ 100 = e^k  ...(2)
Now, if t = 10, then p = 2× 100 = 200.

⇒ r/10 = 0.6931 
⇒ r = 6.931 
Hence, the value of r is 6.93 %.

21. In a bank, principal increases continuously at the rate of 5% per year. An amount of Rs 1000 is deposited with this bank, how much will it worth after 10 years (e^0.5 = 1.648).

Solution

Let p and t be the principal and time respectively. 

It is given that the principal increases continuously at the rate of 5 % per year. 

Now, when t = 0, p = 1000. 
1000 = e^c  ...(2)
At t = 10, years the amount will worth Rs 1648. 

22. In a culture, the bacteria count is 1,00,000. The number is increased by 10% in 2 hours. In how many hours will the count reach 2,00,000, if the rate of growth of bacteria is proportional to the number present?

Solution

Let y be the number of bacteria at any instant t. 

It is given that the rate of growth of the bacteria is proportional to the number peresent. 
∴ dy/dt  ∝ y 
⇒ dy/dt = ky  (where k is a constant) 
⇒ dy/y = kdt 
Integrating both sides, we get:  
∫dy/y = k ∫dt 
⇒ log y = kt + C ...(1) 
Let y₀ be the number of bacteria at t = 0 .
log y₀ be the number of bacteria at t = 0. 
log y₀ = C 
Substituting the value of C in equation (1), we get : 
log y = kt + log y₀ 
⇒ log y - log y₀ = kt 
⇒ log (y/y₀) = kt 
⇒ kt = log (y/y₀) ...(2) 
Also, it is given that the number of bacteria increases by 10% in 2 hours.  
⇒ y = (110/100)y₀ 
⇒ y/y₀ = 11/10 ...(3) 
Substituting this value in equation (2), we get :  
k⋅2 = log (11/10) 
⇒ k = (1/2) log (11/10)
Therefore, equation (2) becomes : 

Now, let the time when the number of bacteria increases from 100000 to 200000 be t₁ . 
y = 2y₀ at t = t₁ 
From equation (4), we get:

Hence, in (2 log 2)/[log (11/10)] hours the number of bacteria increases from 100000 to 200000. 

23. The general solution of the differential equation dy/dx = e^x+y  is
(A) e^x + e^–y = C
(B) e^x + e^y = C
(C) e^–x + e^y = C
(D) e^–x + e^–y = C

Solution

Integrating both sides, we get :  
∫e^–y dy = ∫e^x dx 
⇒ -e^–y = e^x + k 
⇒ e^x + e^–y = -k 
⇒ e^x + e^–y = c     (c = -k ) 
Hence, the correct answer is A.