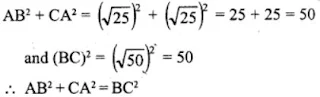RD Sharma Solutions Chapter 14 Coordinate Geometry Exercise 14.2 Class 10 Maths

Chapter Name | RD Sharma Chapter 14 Coordinate Geometry |
Book Name | RD Sharma Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 14.2 Solutions
1. Find the distance between the following pair of points :
(i) (-6, 7) and (-1, -5)
(ii) (a + b, b + c) and (a – b, c – b)
(iii) (a sin α, -b cos α) and (-a cos α, -b sin α)
(iv) (a, 0) and (0, b)
Solution
We know that the distance between two points A(x1, y1) and B(x2, y2) is
2. Find the value of a when the distance between the points (3, a) and (4, 1) is √10
Solution
Distance between (3, a) and (4, 1).
3. If the points (2, 1) and (1, -2) are equidistant from the point (x, y), show that x + 3y = 0.
Solution
4. Find the values of x, y if the distances of the point (x, y) from (-3, 0) as well as from (3, 0) are 4.
Solution
Distance between (x, y) and (-3, 0) is
5. The length of a line segment is of 10 units and the coordinates of one end-point are (2, -3). If the abscissa of the other end is 10, find the ordinate of the other end.
Solution
Let the ordinate of other end by y, then the distance between (2, -3) and (10, y) is
6. Show that the points (-4, -1), (-2, -4), (4, 0) and (2, 3) are the vertices points of a rectangle.
Solution
Let ABCD is a rectangle whose vertices are:
A(-4, -1), B(-2, -4), C(4, 0) and D(2, 3)
AB = CD and AD = BC
and diagonal AC = BD
ABCD is a rectangle
7. Show that the points A (1, -2), B (3, 6), C (5, 10) and D (3, 2) are the vertices of a parallelogram.
Solution
Points are A(1, -2), B(3, 6), C(5, 10) and D(3,2).
∵ AB = CD and AD = BC
∴ ABCD is a parallelogram.
8. Prove that the points A (1, 7), B (4, 2), C (-1, -1) and D (-4, 4) are the vertices of a square.
Solution
Vertices A (1, 7), B (4, 2), C (-1,-1), D (-4, 4)
If these are the vertices of a square, then its diagonals and sides are equal.
∵ AB = BC = CD = DA and AC = BD
∴ ABCD is a square.
9. Prove that the points (3, 0), (6, 4) and (-1, 3) are the vertices of a right-angled isosceles triangle.
Solution
Vertices of ΔABC are A(3, 0), B(6, 4) and C(-1, 3)
We see that, AB = CA and BC is the longest side.
Here, ΔABC is an isosceles right triangle.
10. Prove that (2, -2), (-2, 1) and (5, 2) are the vertices of a right angled triangle. Find the area of the triangle and the length of the hypotenuse.
Solution
Let the vertices of a triangle are A(2, -2), B(-2, 1) and C(5, 2)
We see that, AB = CA and BC is the longest side and AB2 + CA2 = 52 + 52 = 25 + 25 = 50 = BC2
ABC is a right angles triangle.
11. Prove that the points (2a, 4a), (2a, 6a) and (2a + √3a , 5a) are the vertices of an equilateral triangle.
Solution
Vertices of ΔABC are A(2a, 4a), B(2a, 6a) and C(2a+ √3a, 5a)
∵ AB = BC = CA = 2a and an equilateral triangle has three equal sides.
∴ ΔABC is an equilateral triangle.
12. Prove that the points (2, 3), (-4, -6) and (1, 3/2 )do not form a triangle.
Solution
Let the coordinates of three points are A(2, 3), B(-4, -6) and C(1, 2)
∴ These points do not form a triangle.
13. The points A (2, 9), B (a, 5) and C (5, 5) are the vertices of a triangle ABC right angled at B. Find the values of a and hence the area of ∆ABC.
Solution
Given that, the points A (2, 9), B (a, 5) and C (5, 5) are the vertices of a ∆ABC right angled at B.
By Pythagoras theorem, AC² = AB² + BC² …(i)
Now by distance formula,
Here, a ≠ 5, since at a = 5, the length of BC = 0. It is not possible because the sides AB, BC and CA from a right angled triangle.
Now, the coordinates of A, B and C becomes (2, 9), (2, 5) and (5, 5) respectively.
Hence, the required area of ∆ABC is 6 sq. units.