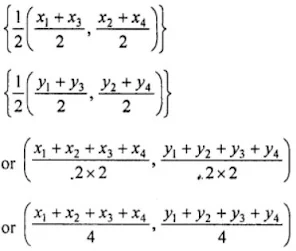RD Sharma Solutions Chapter 14 Coordinate Geometry Exercise 14.4 Class 10 Maths

Chapter Name | RD Sharma Chapter 14 Coordinate Geometry |
Book Name | RD Sharma Mathematics for Class 10 |
Other Exercises |
|
Related Study | NCERT Solutions for Class 10 Maths |
Exercise 14.2 Solutions
1. Find the centroid of the triangle whose vertices are :
(i) (1, 4), (-1, -1), (3, -2)
(ii) (-2, 3), (2, -1), (4, 0)
Solution
(i) Coordinates of the centroid are
2. Two vertices of a triangle are (1, 2), (3, 5) and its centroid is at the origin. Find the Co-ordinates of the third vertex.
Solution
Centroid of a triangle is O(0, 0) …(i)
Co-ordinates of two vertices of a ∆ABC are A (1, 2) and B (3, 5)
Let the third vertex be (x, y)
The vertex is (-4, -7)
3. Find the third vertex of a triangle, if two of its vertices are at (-3, 1) and (0, -2) and the centroid is at the origin.
Solution
Let two vertices of a ∆ABC be A (-3, 1) and B (0, -2) and third vertex C be (x, y)
Centroid of the ∆ABC is O (0, 0)
∴ y = 1
∴ Coordinates of third vertex C are (3, 1)
4. A (3, 2) and B (-2, 1) are two vertices of a triangle ABC whose centroid G has the coordinates (5/3, -1/3) . Find the coordinates of the third vertex C of the triangle.
Solution
A (3, 2) and B (-2, 1) are the two vertices of ∆ABC whose centroid is G (5/3, -1/3)
Let third vertex C be (x, y)
⇒ 3 + x = -1
⇒ x = -1 - 3 = -4
∴ Coordinates of C will be (4, -4)
5. If (-2, 3), (4, -3) and (4, 5) are the mid-points of the sides of a triangle, find the co-ordinates of its centroid.
Solution
In ∆ABC, D, E and F are the mid-points of the sides BC, CA and AB respectively.
The co-ordinates of D are (-2, 3), of E are (4,-3) and of F are (4, 5)
Let the co-ordinates of A, B and C be (x1, y1), (x2, y2), (x3, y3) respectively.
Similarly, E and F are the mid points of AC and AB respectively.
6. Prove analytically that the line segment joining the middle points of two sides of a triangle is equal to half of the third side.
Solution
In ∆ABC,
D and E are the mid points of the sides AB and AC respectively.
7. Prove that the lines joining the middle points of the opposite sides of a quadrilateral and the join of the middle points of its diagonals meet in a point and bisect one another.
Solution
Let A (x1, y1), B (x2, y2), C (x3, y3) and D (x4, y4) be the vertices of quadrilateral ABCD
E and F are the mid points of side BC and AD respectively and EF is joined G and H are the mid points of diagonal AC and BD.
GH are joined.
EF and Gh intersect each other at M.
Let M is the mid-point of EF, then its coordinates will be
Let M is the mid-point of GH, then its coordinates of M will be
We see the coordinates of in both cases are same.
EF and GH bisect each other at M.
Hence, proved.
8. If G be the centroid of a triangle ABC and P be any other point in the plane, prove that PA² + PB² + PC² = GA² + GB² + GC² + 3GP².
Solution
In AABC, G is the centroid of it Let P (h, x) is any point in the plane
Let co-ordinates of A are (x1, y1) of B are (x2, y2) and of C are (x3, y3)
9. If G be the centroid of a triangle ABC, prove that AB² + BC² + CA² = 3 (GA² + GB² + GC²)
Solution
Let the co-ordinates of the vertices of ∆ABC be A (x1, y1), B (x2, y2), C (x3, y3) and let G be the centroid of the triangle.
Hence, proved.
10. In the figure, a right triangle BOA is given. C is the mid-point of the hypotenuse AB. Show that it is equidistant from the vertices O, A and B.
Solution

In right ∆OAB, co-ordinates of O are (0, 0) of A are (2a, 0) and of B are (0, 2b)
C is the mid-point of AB
Co-ordinates of C will be

We see that CO = CA = CB
Hence, C is equidistant from the vertices O, A and B.
Hence, proved.