NCERT Solutions for Class 10 Maths Chapter 6 त्रिभुज 6.3 Hindi Medium

Class 10 Maths Chapter 6 Triangles Exercise 6.3 NCERT Solutions in Hindi Medium

त्रिभुज Ganit NCERT Solutions in Hindi Medium Exercise 6.3

प्रश्न 1. बताइए कि आकृति 6.34 में दिए त्रिभुजों के युग्मों में से कौन - कौन से युग्म समरूप हैं | उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देनें में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए |

Solution

(i) हाँ, ΔABC तथा ΔPQR में

∠ABC = ∠PQR = 80°
∠BAC = ∠QPR = 60°
∠ACB = ∠PRQ = 40°

यहाँ, दोनों त्रिभुज के संगत कोण बराबर होते हैं |

∴ ΔABC ~ ΔPQR (AAA समरूपता कसौटी से)

(ii) हाँ, ΔABC तथा ΔQRP में

यहाँ, सभी संगत भुजाएँ बराबर समानुपात में हैं |

∴ ΔABC ~ ΔQRP (SSS समरूपता कसौटी से)

(iii) नहीं, ΔLMP तथा ΔFED में

यहाँ, सभी संगत भुजाएँ समानुपात में नहीं हैं |

इस प्रकार, ΔLMP तथा ΔFED समानुपात में नहीं हैं |

(iv) हाँ, ΔLMN तथा ΔRQP में

यहाँ, दो समीपवर्ती संगत भुजाएँ समानुपात में हैं और एक कोण समान है |

∴ ΔLMN ~ ΔRQP (SAS समरूपता कसौटी से)

(v) नहीं, ΔABC तथा ΔDEF में

ΔABC में, ∠A दिया परन्तु सम्मिलित भुजा A नहीं दी हुयी है |

(vi) हाँ, ΔDEF तथा ΔPQR में

∠D = 70°, ∠E = 80° तथा ∠F = 30° (∵ ΔDEF में, ∠D + ∠E + ∠F = 180°)

∠Q = 80°, ∠R = 30° तथा ∠P = 70° (∵ ΔQPR में, ∠Q + ∠P + ∠R = 180°)

यहाँ, ∠D = ∠P, ∠E = ∠Q, ∠F = ∠R

∴ ΔDEF ~ ΔQPR (AAA समरूपता कसौटी से)

प्रश्न 2. आकृति 6.35 में, ΔODC ~ ΔOBA, ∠BOC = 125o और ∠CDO = 70o है | ∠DOC, ∠DCO और ∠OAB ज्ञात कीजिए |

Solution

∠DOC + ∠BOC = 180° (∵ DOB एक सरल रेखा है)

⇒ ∠DOC +125^o = 180°

⇒ ∠DOC = 180° -125^o

⇒ ∠DOC = 55^o

अब ΔDOC में,

 ∠DOC + ∠CDO + ∠DCO = 180° (त्रिभुज के तीनों कोणों का योग)

⇒ 55^o + 70^o + ∠DCO = 180°

⇒ 125^o ∠DCO = 180°

⇒ ∠DCO = 180° - 125^o

⇒ ∠DCO = 55^o

ΔODC ~ ΔOBA (दिया है)

∴ ∠OAB = ∠DCO = 55^o

अतः ∠OAB = ∠DCO = ∠DOC = 55^o

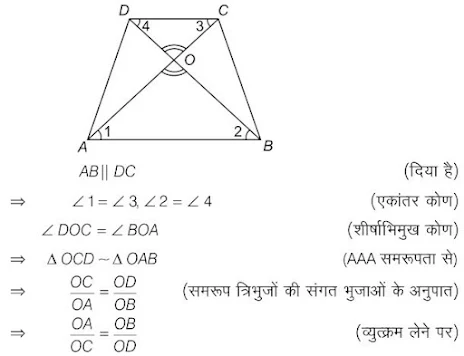
प्रश्न 3. समलंब ABCD, जिसमे AB || DC है, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं | दो त्रिभुजों की समरूपता कसौटी का प्रयोग करते हुए दर्शाइए कि OA/OC = OB/OD है |

Solution

दिया है: समलंब चतुर्भुज के विकर्ण और परस्पर बिंदु पर प्रतिच्छेद करते हैं |

सिद्ध करना है: OA/OC = OB/OD

प्रश्न 4. आकृति में, QR/QS = QT/PR तथा ∠1 = ∠2 है | दर्शाइए कि ∆PQS ～ ∆TQR है |

Solution

चित्र में,

∠1 = ∠2 (दिया है)
⇒ PQ =PR (ΔPQR के समान कोणों कि विपरीत भुजाएँ)