NCERT Solutions for Class 10 Maths Chapter 6 त्रिभुज 6.4 Hindi Medium

Class 10 Maths Chapter 6 Triangles Exercise 6.4 NCERT Solutions in Hindi Medium

त्रिभुज Ganit NCERT Solutions in Hindi Medium Exercise 6.4

प्रश्न 1. मान लीजिए ΔABC ~ ΔDEF और इनके क्षेत्रफल क्रमशः 64cm² और 121cm² हैं | यदि EF = 15.4 cm² हो, तो BC ज्ञात कीजिए |

Solution

दिया गया है, ΔABC ~ ΔDEF

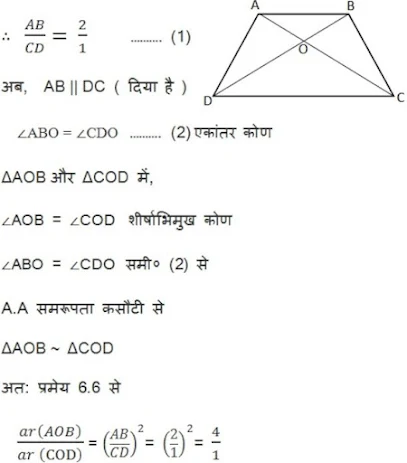
प्रश्न 2. एक समलंब ABCD जिसमें AB || DC हैं, के विकर्ण परस्पर बिन्दु O पर प्रतिच्छेद करते हैं | यदि AB = 2 CD हो तो ΔAOB और ΔCOD के क्षेत्रफलों का अनुपात ज्ञात कीजिए |

Solution

ABCD एक समलंब है जिसमें AB || DC हैं, के विकर्ण परस्पर बिन्दु O पर प्रतिच्छेद करते हैं |
और AB = 2 CD (दिया है)

ΔAOB और ΔCOD के क्षेत्रफलों का अनुपात 4:1 है| 

प्रश्न 3. आकृति 6.44 में एक ही आधार BC पर दो त्रिभुज ABC और DBC बने हुए हैं | यदि AD,BC कोप O पर प्रतिच्छेद करे, तो दर्शाइए की ar(ABC)/ar(DBC) = AO/DO है |

Solution

AL ⊥ BC तथा DM ⊥ BC खींचा ∆OLA तथा ∆OMD में,

∠ALO = ∠DMO = 90°

तथा ∠AOL = ∠DOM (शीर्षाभिमुख कोण)

∴ ΔOLA ~ ΔOMD (AA समरूपता से)

प्रश्न 4. यदि दो समरूप तत्रिभुजों के क्षेत्रफल बराबर हों तो सिद्ध कीजिए कि वे त्रिभुज सर्वान्गसम होते हैं|

Solution

दिया है,
ΔABC ~ ΔPQR तथा ar (ΔABC) = ar (ΔPQR)

(समरूप त्रिभुजों के क्षेत्रफल के गन से)
⇒ AB = PQ, BC = QR CA = PR (SSS अनुपातिक मापदंड से)
⇒ ΔABC ~ ΔPQR 

प्रश्न 5. एक त्रिभुज ABC की भुजाओं AB,BC और CA के मध्य - बिन्दु क्रमशः D, E और F हैं | त्रिभुज DEF और त्रिभुज ABC के क्षेत्रफलों का अनुपात ज्ञात कीजिए|

Solution

ΔABC की भुजाओं AB, AC तथा CA के मध्य-बिंदु D, E तथा F को लेते हुए एक ΔDEF बनाया |

अतः अभीष्ट अनुपात 1:4 है |

प्रश्न 6. सिद्ध कीजिए कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात इनकी संगत माध्यिकाओं के अनुपात का वर्ग होता है |

Solution

चित्र में AD, ΔABC की माध्यिका और PM, ΔPQR की माध्यिका है |

यहाँ D तथा M क्रमशः BC और QR का मध्य-बिंदु है |

प्रश्न 7. सिद्ध कीजिए कि दो एक वर्ग की किसी भुजा पर बनाए गए समबाहु त्रिभुज का क्षेत्रफल उसी वर्ग के एक विकर्ण पर बनाए गए समबाहु त्रिभुज के क्षेत्रफल का आधा होता है |

Solution

ABCD एक वर्ग है जिसकी भुजा की लम्बाई = a
तब, विकर्ण BD = a√2

ΔPAB तथा ΔQBD समबाहु त्रिभुज है|

ΔPAB ~ ΔQBD

प्रश्न 8. ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कोई भुजद BC का मध्य-बिन्दु है | त्रिभुजों ABC और BDE के क्षेत्रफलों का अनुपात है:

(A) 2:1

(B) 1:2

(C) 4:1

(D) 1:4

Solution

(c) यहाँ  AB = BC = CA = a (माना)
Δ एक समबाहु त्रिभुज है|

अतः ΔABC और ΔBDE के क्षेत्रफलों का अनुपात = 4 : 1

प्रश्न 9. दो समरूप त्रिभुजों की भुजाएँ 4:9 के अनुपात में हैं | इन त्रिभुजों के क्षेत्रफलों का अनुपात है :

(A) 2:3

(B) 4:9

(C) 81:16

(D) 16: 81

Solution

(d) दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी सांगत भुजाओं के वर्गों के अनुपात के बराबर होता है |

∴ त्रिभुजों के का क्षेत्रफलों अनुपात = (4/9)² = 16:81