Class 9 Maths Chapter 8 Quadrilaterals 8.1 NCERT Solutions in Hindi Medium

चतुर्भुज Ganit NCERT Solutions in Hindi Medium Exercise 8.1
प्रश्न 1. एक चतुर्भुज के कोण 3 : 5 : 9 : 13 के अनुपात में हैं | इस चतुर्भुज के सभी कोण ज्ञात कीजिए |
Solution
दिया है, चतुर्भुज के कोण 3 : 5 : 9 : 13 के अनुपात में है|
माना चतुर्भुज के 3x, 5x, 9x तथा 13x है |
हम जानते हैं कि किसी चतुर्भुज के चारों कोणों का योग 360° होता है|
∴ 3x + 5x + 9x + 13x = 360°
⇒ 30x = 360°
अत: सभी कोण,
3x = 3 × 12° = 36°
5x = 5 × 12° = 60°
9x = 9 × 12° = 108°
13x = 13 × 12° = 156°
प्रश्न 2. यदि एक समांतर चतुर्भुज के विकर्ण बराबर हों, तो दर्शाइए कि वह एक आयत है |
Solution
ABCD एक समांतर चतुर्भुज है जिसके विकर्ण AC = BD है |

सिद्ध करना है : ABCD एक आयत है |
प्रमाण : ΔABD तथा ΔABC में
AD = BC (समांतर चतुर्भुज की सम्मुख भुजा)
AB = AB (उभयनिष्ठ)
BD = AC (दिया है)
SSS सर्वांगसमता नियम से,
ΔABD ≅ ΔABC
∴ ∠A = ∠B (CPCT से) ...(i)
चूँकि ABCD एक समांतर चतुर्भुज है |
∴ AD || BC और AB एक तिर्यक रेखा है |
अत: ∠A + ∠B = 180° (अंत: आसन्न कोणों का योग)
⇒∠A + ∠A = 180° ...समीo (i) से
⇒ 2∠A = 180°
⇒ ∠A = 90° (वह समांतर चतुर्भुज जिसकी एक कोण समकोण हो आयत कहलाता है)
अत: ABCD एक आयत है |
प्रश्न 3. दर्शाइए कि यदि एक चतुर्भुज के विकर्ण परस्पर समकोण पर समद्विभाजित करें, तो वह एक समचतुर्भुज होता है।
Solution
ABCD एक चतुर्भुज है जिसके विकर्ण AC तथा BD एक दुसरे को बिंदु O पर समद्विभाजित करते हैं | जहाँ ∠COD = 90° है और AO = CO तथा BO = DO है |

सिद्ध करना है : ABCD एक आयत है |
प्रमाण : ΔAOB तथा ΔCOD में
AO = CO (दिया है)
BO = DO (दिया है)
∠AOB = ∠COD (शिर्षाभिमुख कोण)
अत: SAS सर्वांगसमता नियम से,
ΔAOB ≅ ΔCOD
∴ AB = CD (CPCT से) …(i)
तथा, ∠BAO = ∠DCO (एकांतर कोण) (CPCT से)
∴ AB || CD ...(ii) (एकांतर कोण बराबर हो तो रेखाएँ समांतर होती है)
समीo (i) तथा (ii) से,
ABCD एक समांतर चतुर्भुज है | (यदि किसी चतुर्भुज की सम्मुख भुजाओं का एक युग्म बराबर एवं समान्तर हो तो वह समान्तर चतुर्भुज होता है |)
∴ AD = BC ...(iii) (समांतर चतुर्भुज की सम्मुख भुजा बराबर होती है)
अब ΔAOD तथा ΔCOD में,
AO = CO (दिया है)
DO = DO (उभयनिष्ठ)
∠AOD = ∠COD (90° प्रत्येक)
अत: SAS सर्वांगसमता नियम से, ΔAOD ≅ ΔCOD
∴ AD = CD (CPCT से) ...(iv)
समीo (i), (iii) तथा (iv) से हम पाते हैं |
AB = BC = CD = AD
अत: ABCD एक समचतुर्भुज है |
(वह समान्तर चतुर्भुज जिसकी प्रत्येक भुजा बराबर हो समचतुर्भुज होता है |)
प्रश्न 4. दर्शाइए कि एक वर्ग के विकर्ण बराबर होते हैं और परस्पर समकोण पर समद्विभाजित करते हैं |
Solution
दिया है : ABCD एक वर्ग है जिसके विकर्ण AC तथा BD एक दुसरे को बिंदु O पर प्रतिच्छेद करते है |
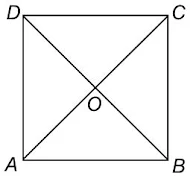
सिद्ध करना है :
(i) AO = CO तथा BO = DO
(ii) AOB = 90°
प्रमाण: ΔAOB तथा ΔCOD में,
AB = CD (वर्ग की भुजा)
∠BAO = ∠DCO (एकांतर कोण)
∠AOB = ∠COD (शिर्षाभिमुख कोण)
अत: ASA सर्वांगसमता नियम से,
ΔAOB ≅ ΔCOD
∴ AO = CO तथा BO = DO (CPCT से) ...(i)
पुन: ΔAOB तथा ΔBOC में,
AB = BC (वर्ग की भुजा)
BO = BO (उभयनिष्ठ)
AO = CO [समीo (i) से]
अत: SSS सर्वांगसमता नियम से, ΔAOB ≅ ΔBOC
अत: ∠AOB = ∠COB (CPCT से) ...(ii)
अब ∠AOB + ∠COB = 180° (रैखिक युग्म)
⇒ ∠AOB + ∠AOB = 180° [समी0 (ii) से]
⇒2∠AOB = 180°
⇒∠AOB = 90°
प्रश्न 5. दर्शाइए कि यदि एक चतुर्भुज के विकर्ण बराबर हो और परस्पर समद्विभाजित करें, तो वह एक वर्ग होता है |
Solution
दिया है : ABCD एकचतुर्भुज है जिसमें विकर्ण AC = BD है और एक दुसरे को बिंदु O पर प्रतिच्छेद करते है | जहाँ AO = CO तथा BO = DO है |
सिद्ध करना है : ABCD एक वर्ग है |
प्रमाण : ΔAOB तथा ΔCOD में,
AO = CO (दिया है)
BO = DO (दिया है)
∠AOB = ∠COD (शिर्षाभिमुख कोण)
अत: SAS सर्वांगसमता नियम से, ΔAOB ≅ ΔCOD
∴ AB = CD (CPCT से) ...(i)
तथा ∠BAO = ∠DCO (एकांतर कोण) (CPCT से)
∴ AB || CD ...(ii) (एकांतर कोण बराबर हो तो रेखाएँ समांतर होती है)
समीo (i) तथा (ii) से, ABCD एक समांतर चतुर्भुज है |
(यदि किसी चतुर्भुज की सम्मुख भुजाओं का एक युग्म बराबर एवं समान्तर हो तो वह समान्तर चतुर्भुज होता है |)∴ AD = BC ...(3) (समांतर चतुर्भुज की सम्मुख भुजा बराबर होती है)
अब ΔAOD तथा ΔCOD में,
AO = CO (दिया है)
DO = DO (उभयनिष्ठ)
∠AOD = ∠COD (90° प्रत्येक)
अत: SAS सर्वांगसमता नियम से, ΔAOD ≅ ΔCOD
∴ AD = CD (CPCT से) ...(iv)
समीo (i), (iii) तथा (iv) से हम पाते हैं,
AB = BC = CD = AD ...(v)
अब ΔABD तथा ΔABC में,
AD = BC (वर्ग की सम्मुख भुजा)
AB = AB (उभयनिष्ठ)
BD = AC (दिया है)
SSS सर्वांगसमता नियम से,
ΔABD ≅ ΔABD
∴ ∠A = ∠B (CPCT से) ...(vi)
चूँकि ABCD एक वर्ग है |
∴ AD || BC और AB एक तिर्यक रेखा है |
अत: ∠A + ∠B = 180° (अंत: आसन्न कोणों का योग)
⇒ ∠A + ∠A = 180° ...समीo (vi) से
⇒ 2∠A = 180°
⇒ ∠A = 180°/2
⇒ ∠A = 90°
⇒ ∠A = 90o ...(vii)
समीo (v) तथा (vii) से स्पष्ट है कि ABCD एक वर्ग है |
प्रश्न 6. समांतर चतुर्भुज ABCD का विकर्ण AC कोण A को समद्विभाजित करता है | (देखिये आकृति 8.19)

दर्शाइए कि:
(i) यह ∠C को भी समद्विभाजित करता है |
(ii) ABCD एक समचतुर्भुज है |
Solution
दिया है : ABCD एक समांतर चतुर्भुज है जिसका विकर्ण AC कोण A को समद्विभाजित करता है |
सिद्ध करना है :
(i) AC, ∠C को भी समद्विभाजित करता है |
(ii) ABCD एक समचतुर्भुज है |
प्रमाण:
(i) ΔABC तथा ΔDAC में,
∠BAC = ∠BAC (दिया है)
∠B = ∠D (समांतर चतुर्भुज के सम्मुख कोण बराबर होते है)
AC = AC (उभयनिष्ठ)
अत: ASA सर्वांगसमता नियम से,
ΔABC ≅ ΔDAC
∴ ∠BCA = ∠DCA (CPCT से)
अत: विकर्ण AC, ∠C को समद्विभाजित करता है |
(ii) पुन: AB = AD (CPCT से) ...(i)
चूँकि ABCD एक समांतर चतुर्भुज है |
∴ AB = CD (समांतर चतुर्भुज की सम्मुख भुजा) ...(ii)
और, BC = AD (समांतर चतुर्भुज की सम्मुख भुजा ) ...(iii)
समीकरण (i), (ii) तथा (iii) से,
AB = BC = CD = AD
अत: ABCD एक समचतुर्भुज है |
प्रश्न 7. ABCD एक समचतुर्भुज है | दर्शाइए कि AC कोणों A और C दोनों को समद्विभाजित करता है तथा विकर्ण BD कोणों B तथा D दोनों को समद्विभाजित करता है |
Solution
दिया है: ABCD एक समचतुर्भुज है।
∴ AD = AB = BC = CD ...(i)

सिद्ध करना है:
(i) विकर्ण AC कोण A के साथ-साथ C को भी समद्विभाजित करता है।
(ii) विकर्ण BD कोण B के साथ-साथ D को भी समद्विभाजित करता है।
प्रमाण:
(i) माना ABCD एक समचतुर्भुज है, जिसके विकर्ण AC तथा BD हैं।
∆ABC तथा ∆ADC में,
AD = AB (दिया है)
CD = BC [समी (i) से]
तथा, AC = CA (उभयनिष्ठ)
∴ ∆ABC ≌ ∆ADC (SSS नियम से)
∴ ∠DAC = ∠BAC (CPCT से)
तथा, ∠DCA = ∠BCA (दिया है)
साथ ही, ∠DAC = ∠DCA
तथा, ∠BAC = ∠BCA
यह प्रदर्शित करता है कि विकर्ण AC कोण A के साथ-साथ C को भी समद्विभाजित करता है।
(ii) पुन: ∆BDC तथा ∆BDA में,
AB = BC (दिया है)
AD = CD (दिया है)
BD = BD (उभयनिष्ठ)
∴ ∆BDC ≌ ∆BDA (SSS नियम से)
∴ ∠BDA = ∠BDC (CPCT से)
तथा, ∠DBA = ∠DBC
साथ ही, ∠BDA = ∠DBA
तथा, ∠BDC = ∠DBC
यह प्रदर्शित करता है कि विकर्ण BD कोण B के साथ-साथ D को भी समद्विभाजित करता है।
प्रश्न 8. ABCD एक आयत है जिसमें विकर्ण AC दोनों कोण A और C को समद्विभाजित करता है | दर्शाइए कि:
(i) ABCD एक वर्ग है |
(ii) विकर्ण BD दोनों कोण B और D को समद्विभाजित करता है |
Solution
दिया है: ABCD एक आयत है।
∴ AB = CD तथा BC = AD ...(i)

सिद्ध करना है:
(i) ABCD एक वर्ग है।
अर्थात् AB = BC = CD = DA
(ii) विकर्ण BD, ∠B के साथ-साथ कोण D को भी A समद्विभाजित करता है।
प्रमाण:
(i) ∆ADC तथा ∆ABC में दिया है,
AB || DC तथा एक तिर्यक रेखा AC इन्हें प्रतिच्छेद करती है।
∠DAC = ∠BAC
∠DCA = ∠BCA
तथा, AC = CA (उभयनिष्ठ)
∴ ∆ADC ≌ ∆ABC (ASA नियम से)
∴ AD = AB (CPCT से)
तथा, CD = BC ...(ii)
अतः समी (i) तथा (ii) से,
AB = BC = AD = CD
∴ ABCD एक वर्ग है।
(ii) ∆AOB तथा ∆COB में दिया है,
AB = BC (वर्ग की भुजा)
BO = OB (उभयनिष्ठ)
OA = OC (∵ वर्ग के विकर्ण एक-दूसरे को समद्विभाजित करते हैं)
∴ ∆AOB ≌ ∆COB (SSS नियम से)
∴ ∠OBA = ∠OBC (CPCT से)
यह प्रदर्शित करता है कि BO या BD कोण B को समद्विभाजित करता है।
इसी प्रकार, ∆AOD तथा ∆COD में, दिया है
AD = CD (वर्ग की भुजा)
OD = DO (उभयनिष्ठ)
तथा, OA = OC (∵ वर्ग के विकर्ण एक-दूसरे को समद्विभाजित करते हैं)
∆AOD ≌ ∆COD (SSS नियम से)
∠ADO = ∠CDO (CPCT से)
यह प्रदर्शित करता है कि DO या DB कोण D को समद्विभाजित करता है।
प्रश्न 9. समांतर चतुर्भुज ABCD के विकर्ण BD पर दो बिंदु P और Q इस प्रकार स्थित हैं कि DP = BQ है। (देखिये आकृति 8.20)

दर्शाइए कि:
(i) ΔAPD ≅ ΔCQB
(ii) AP = CQ
(iii) ΔAQB ≅ ΔCPD
(iv) AQ = CP
(v) APCQ एक समान्तर चतुर्भुज है |
Solution
दिया है: ABCD एक समांतर चतुर्भुज है और DP = BQ है |
सिद्ध करना है:
(i) ΔAPD ≅ ΔCQB
(ii) AP = CQ
(iii) ΔAQB ≅ ΔCPD
(iv) AQ = CP
(v) APCQ एक समान्तर चतुर्भुज है |
प्रणाम:
(i) ΔAPD तथा ΔCQB में
AD = BC (समांतर चतुर्भुज की सम्मुख भुजा)
DP = BQ (दिया है)
∠ADP = ∠CBQ (एकांतर अत: कोण)
अत: S.A.S सर्वांगसमता नियम से,
∴ ΔAPD ≅ ΔCQB
(ii) अत: AP = CQ ...(i) (CPCT से/सर्वांगसम त्रिभुज के संगत भाग)
(iii) ΔAQB तथा ΔCPD में,
AB = DC (समांतर चतुर्भुज की सम्मुख भुजा)
BQ = DP (दिया है)
∠ABQ = ∠CDP (एकांतर अत: कोण)
अत: S.A.S सर्वांगसमता नियम से,
∴ ΔAQB ≅ ΔCPD
(iv) अत: AQ = CP ...(ii) (CPCT से/सर्वांगसम त्रिभुज के संगत भाग)
(v) समीo (i) तथा (ii) से,
APCQ एक समान्तर चतुर्भुज है |
प्रश्न 10. ABCD एक समांतर चतुर्भज है तथा AP और CQ शीर्षों A और C से विकर्ण BD पर क्रमशः लम्ब हैं। (देखिये आकृति 8.21)
दर्शाइए कि:
(i) Δ APB ≅ Δ CQD
(ii) AP = CQ
Solution
दिया है, ABCD एक समान्तर चतुर्भुज है तथा AP और CQ क्रमशः शीर्षों A और C से विकर्ण BD पर लम्ब हैं।
∵ AB || CD तथा BD एक तिर्यक रेखा है।
∴ ∠CDB = ∠DBA ...(i)
(i) अब, ΔAPB तथा ΔCQD में, दिया है
CD = AB (समान्तर चतुर्भुज की भुजाएँ हैं)
∠CQD = ∠APB = 90° (दिया है)
∠CDQ = ∠ABP [समी (i) से]
∴ ΔAPB ≅ ΔCQD (ASA नियम से)
(ii) ∵ ΔAPB ≅ ΔCQD
∴ AP = CQ (CPCT से)
प्रश्न 11. ΔABC और ΔDEF में, AB = DE, AB||DF, BC = EF और BC||EF है | शीर्षों A, B और C को क्रमश: शीर्षों D, E और F से जोड़ा जाता है | (देखिये आकृति 8.22)
दर्शाइए कि:
(i) चतुर्भुज ABED एक समांतर चतुर्भुज है।
(ii) चतुर्भुज BEFC एक समांतर चतुर्भुज है।
(iii) AD || CF और AD = CF है|
(iv चतुर्भुज ACFD एक समांतर चतुर्भुज है।
(v) AC = DF है |
(vi) ΔABC ≅ ΔDEF है |
Solution
दिया है, ΔABC तथा ΔDEF में,
AB = DE, AB || DE
तथा, BC = EF, BC || EF
(i) अब, चतुर्भुज ABED में,
AB = DE तथा AB || DE (दिया है)
⇒ ABED एक समान्तर चतुर्भुज है। (∵ सम्मुख भुजाओं का युग्म बराबर तथा समान्तर होते हैं)
(ii) चतुर्भुज BEFC में,
BC = EF तथा BC || EF
⇒ BEFC एक समान्तर चतुर्भुज है। (∵ सम्मुख भुजाओं का युग्म बराबर तथा समान्तर होते हैं)
(iii) चूँकि ABED एक समान्तर चतुर्भुज है।
∴ AD || BE तथा AD = BE ...(i)
साथ ही, BEFC एक समान्तर चतुर्भुज है।
∴ CF || BE तथा CF = BE ...(ii)
समी (i) तथा (ii) से,
AD || CF तथा AD = CF
(iv) चतुर्भुज ACFD में, दिया है
AD || CF तथा AD = CF [भाग (iii) से]
⇒ ACFD एक समान्तर चतुर्भुज है।
(v) चूँकि ACFD एक समान्तर चतुर्भुज है।
∴ AC = DF तथा AC || DF
(vi) अब, ΔABC तथा ΔDEF में,
AB = DE (दिया है)
BC = EF (दिया है)
तथा, AC = DF [भाग (v) से]
∴ ΔABC ≅ ΔDEF (SSS नियम से)
प्रश्न 12. ABCD एक समलम्ब है, जिसमें AB || DC और AD = BC है | (देखिये आकृति 8.23)
दर्शाइए कि:
(i) ∠ A = ∠ B
(ii) ∠ C = ∠ D
(iii) ΔABC ≅ ΔBAD
(iv) विकर्ण AC = विकर्ण BD है |
Solution
दिया है, ABCD एक समलम्ब चतुर्भुज है।
AB || CD तथा AD = BC
अब, रेखा AB का विस्तार करते हैं तथा एक रेखा CE खींचते हैं जो AD के समान्तर है। रेखा CE, AB के बढ़े हुए भाग के बिन्दु E पर मिलती है।
अब, ADCE एक समान्तर चतुर्भुज है।
∴ AD || CE तथा AD = CE
परन्तु, AD = BC
∴ AD = BC = CE
(i) हम जानते हैं कि, ∠A + ∠E = 180° (∵ तिर्यक रेखा AE के एक ही ओर के अन्तः कोण हैं)
⇒ ∠E = 180° – ∠A
चूँकि, BC = EC
∴ ∠E = ∠CBE = 180° – ∠A
साथ ही, ∠ABC = 180° – ∠CBE (∵ ABE एक सरल रेखा है)
= 180° – 180° + ∠A
⇒ ∠B = ∠A ...(i)
(ii) अब, ∠A+ ∠D = 180° (∵ तिर्यक रेखा AD के एक ही ओर के अन्तः कोण हैं)
⇒ ∠D = 180° – ∠A
⇒ ∠D = 180° – ∠B [समी (i) से] ...(ii)
साथ ही, ∠C + ∠B = 180° (∵ तिर्यक रेखा BC के एक ही ओर के अन्तः कोण हैं)
⇒ ∠C = 180° – ∠B ...(iii)
समी (ii) तथा (iii) से,
∠C = ∠D
(iii) अब, ΔABC तथा ΔBAD में दिया है,
AB = BA (उभयनिष्ठ)
AD = BC (दिया है)
∠A = ∠B [समी (i) से]
∴ ΔABC ≅ ΔBAD (SAS नियम से)
(iv) चूँकि, ΔABC ≅ ΔBAD (ऊपर सिद्ध कर चुके है
∴ AC = BD (CPCT से)





