Class 9 Maths Chapter 8 Quadrilaterals 8.2 NCERT Solutions in Hindi Medium
चतुर्भुज Ganit NCERT Solutions in Hindi Medium Exercise 8.2
प्रश्न 1. ABCD एक चतुर्भुज है जिसमें P, Q, R और S क्रमश: भुजाओं AB, BC, CD और DA के मध्य-बिंदु हैं | AC उसका एक विकर्ण है | (देखिये आकृति 8.29)
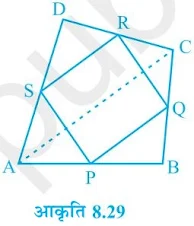
दर्शाइए कि:
(i) SR || AC और SR = 1/2 AC है |
(ii) PQ = SR है।
(iii) PQRS एक समान्तर चतुर्भुज है ।
Solution
दिया है, P, Q, R और S क्रमशः भुजाओं AB, BC, CD तथा DA के मध्य-बिन्दु हैं।
∴ AP = PB, BQ = CQ
CR = DR तथा AS = DS
(i) ΔADC में, दिया है
S भुजा AD का मध्य-बिन्दु है तथा R भुजा DC का मध्य-बिन्दु है।
हम जानते हैं कि किसी त्रिभुज में दो भुजाओं के मध्य - बिन्दु को मिलाने वाला रेखाखण्ड तीसरी भुजा के समान्तर होता है।
∴ SR || AC ...(i)
साथ ही, SR = ½ AC ...(ii)
(ii) इसी प्रकार, ΔABC में, दिया है
PQ || AC ...(iii)
तथा, PQ = ½ AC ...(iv)
अब, समी (ii) तथा (iv) से,
SR = PQ = ½ AC ...(v)
(iii) अब, समी (i) तथा (iii) से,
PQ || SR
तथा समी (v) से, PQ = SR
चूँकि चतुर्भुज PQRS की सम्मुख भुजाओं का युग्म बराबर तथा समान है।
इसलिए PQRS एक समान्तर चतुर्भुज है।
प्रश्न 2. ABCD एक समचतुर्भुज है और P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिंदु है। दर्शाइए कि चतुर्भुज PQRS एक आयत है।
Solution
दिया है, ABCD एक समचतुर्भुज है और P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिन्दु हैं।

मध्य-बिन्दु प्रमेय से,

∴ PQRS एक समान्तर चतुर्भुज है।
अब, हम जानते हैं कि समचतुर्भुज के विकर्ण एक-दूसरे को समकोण पर समद्विभाजित करते हैं।
∴ ∠EOF = 90°
अब, RQ || BD (मध्य-बिन्दु प्रमेय से)
⇒ RE || OF
साथ ही, SR || AC [समी (i) से]
⇒ FR || OE
∴ OERF एक समान्तर चतुर्भुज है।
इसलिए,
∠ERF = ∠EOF = 90° (चतुर्भुज के सम्मुख कोण बराबर होते हैं)
इस प्रकार, PQRS एक समान्तर चतुर्भुज है, जिसमें ∠R = 90°
अतः PQRS एक आयत है।
प्रश्न 3. ABCD एक आयत है, जिसमें P, Q, R और S क्रमश: भुजाओं AB, BC, CD और DA के मध्य-बिंदु हैं | दर्शाइए कि चतुर्भुज PQRS एक समचतुर्भुज है |
Solution
दिया है, ABCD एक आयत है।

∠A = ∠B = ∠C = ∠D = 90°
तथा, AD = BC, AB = CD
साथ ही P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिन्दु हैं।

आयत ABCD में,
AC = BD
∴ PQ = SR ...(i)
अब, ΔASP तथा ΔBQP में,
AP = BP (दिया है)
AS = BQ (दिया है)
∠A = ∠B (दिया है)
∴ ΔASP ≅ ΔBQP (SAS नियम से)
∴ SP = PQ (CPCT से) ...(ii)
इसी प्रकार, ΔRDS तथा ΔRCQ में,
SD = CQ (दिया है)
DR = RC (दिया है (दिया है))
∠C = ∠D (दिया है)
ΔRDS ≅ ΔRCQ (SAS नियम से)
SR = RQ (CPCT से) ...(iii)
समी (i), (ii) तथा (iii) से स्पष्ट है कि चतुर्भुज PQRS एक समचतुर्भुज है।
प्रश्न 4. ABCD एक समलंब है, जिसमें AB || DC है। साथ ही, BD एक विकर्ण है और E भुजा AD का मध्य-बिंदु है। E से होकर एक रेखा AB के समांतर खींची गई है, जो BC को F पर प्रतिच्छेद करती है । दर्शाइए कि F भुजा BC का मध्य-बिंदु है। (देखिये आकृति 8.30)
Solution
दिया है : ABCD एक समलंब है, जिसमें AB || DC है।
साथ ही, BD एक विकर्ण है और E भुजा AD का मध्य-बिंदु है। E से होकर एक रेखा AB के समांतर खींची गई है, जो BC को F पर प्रतिच्छेद करती है ।
सिद्ध करना है: CF = BF
रचना: D को B से मिलाया जो EF को P पर प्रतिच्छेद करता है |
प्रमाण:
ΔABD में,
AB || EF ...(i) (दिया है)
और E भुजा AD का मध्य-बिंदु है |
(किसी त्रिभुज की एक भुजा के मध्य-बिंदु से दूसरी भुजा के समांतर खिंची गई रेखा तीसरी भुजा को समद्विभाजित करती है)
अत: मध्य-बिंदु प्रमेय 8.10 से,
इसलिए बिंदु P भुजा BD का मध्य-बिंदु है | ...(i)
अब AB || CD ...(ii) (दिया है)
समीकरण (i) तथा (ii) से,
CD || EF और बिंदु P भुजा BD का मध्य-बिंदु है [समीकरण (i) से]
अत: मध्य-बिंदु प्रमेय 8.10 से ΔBCD में,
F भुजा BC का मध्य-बिंदु है |
इसलिए CF = BF
प्रश्न 5. एक समांतर चतुर्भुज ABCD में E और F क्रमश: भुजाओं AB और CD के मध्य-बिंदु हैं | दर्शाइए कि रेखाखंड AF और EC विकर्ण BD को समत्रिभाजित करते हैं |
Solution
दिया है: एक समांतर चतुर्भुज ABCD में E और F क्रमश: भुजाओं AB और CD के मध्य-बिंदु हैं |
सिद्ध करना है: DP = PQ = QB
प्रमाण:
ΔABP में,
E भुजा AB का मध्य-बिंदु है और AF||EC दिया है |
अत: मध्य-बिंदु प्रमेय 8.10 से,
Q भुजा PB का मध्य-बिंदु है |
अत: PQ = QB ...(i)
(किसी त्रिभुज की एक भुजा के मध्य-बिंदु से दूसरी भुजा के समांतर खिंची गई रेखा तीसरी भुजा को समद्विभाजित करती है)
अब, ΔCDQ में,
F भुजा CD का मध्य-बिंदु है और AF||EC दिया है |
अत: मध्य-बिंदु प्रमेय 8.10 से,
P भुजा DQ का मध्य-बिंदु है |
इसलिए, DP = PQ ...(ii)
समीकरण (i) तथा (ii) से
DP = PQ = QB
प्रश्न 6. दर्शाइए कि किसी चतुर्भुज की सम्मुख भुजाओं के मध्य-बिंदुओं को मिलाने वाले रेखाखंड परस्पर समद्विभाजित करते हैं।
Solution
दिया है: ABCD एक चतुर्भुज है जिसके भुजाएँ AB, BC, CD और DA का मध्य-बिंदु क्रमश: P, Q, R और S है |
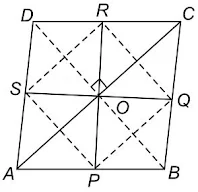
सिद्ध करना है: विकर्ण PR और SQ एक दुसरे को समद्विभाजित करते हैं |
रचना: P, Q, R और S को मिलाया और A को C से मिलाया |
प्रमाण: त्रिभुज ADC में AD तथा CD का मध्यबिंदु क्रमश: S तथा R है | (दिया है)
अतः मध्य-बिंदु प्रमेय से,
इसलिए, SR || AC और SR = ½ AC ...(i)
त्रिभुज ABC में,
AB तथा BC का मध्य-बिंदु P तथा Q है | (दिया है)
इसलिए मध्य-बिंदु प्रमेय से,
PQ || AC और PQ = ½ AC ...(ii)
समीकरण (i) तथा (ii) से
SR || PQ और SR = PQ
अर्थात, PQ = SR
(यदि किसी चतुर्भुज के सम्मुख भुजाओं के एक युग्म में से कोई भी एक युग्म बराबर और समान्तर हो तो वो समान्तर चतुर्भुज होता है)
इसलिए PQRS एक समान्तर चतुर्भुज है |
अब चूँकि PQRS एक समांतर चतुर्भुज है तो इसके विकर्ण PR और SQ एक दुसरे को समद्विभाजित करते हैं |
(समांतर चतुर्भुज के विकर्ण एक दुसरे को समद्विभाजित करते है |)
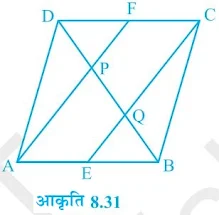
प्रश्न 7. ABC एक त्रिभुज है जिसका कोण C समकोण है | कर्ण AB के मध्य-बिंदु M से होकर BC के समांतर खिंची गई रेखा AC को D पर प्रतिच्छेद करती है | (देखिये आकृति 8.31)
दर्शाइए कि:
(i) D भुजा AC का मध्य-बिंदु है |
(ii) MD ⊥ AC है |
(iii) CM = MA = ½ AB है |
Solution
दिया है: ABC एक त्रिभुज है जिसका कोण C समकोण है | कर्ण AB के मध्य-बिंदु M से होकर BC के समांतर खिंची गई रेखा AC को D पर प्रतिच्छेद करती है |

सिद्ध करना है:
(i) D भुजा AC का मध्य-बिंदु है |
(ii) MD ⊥ AC है |
(iii) CM = MA = ½ AB है |
प्रमाण:
(i) ΔABC में,
M भुजा AB का मध्य-बिंदु है और MD || BC है |
अत: मध्य-बिंदु प्रमेय 8.10 से,
(किसी त्रिभुज की एक भुजा के मध्य-बिंदु से दूसरी भुजा के समांतर खिंची गई रेखा तीसरी भुजा को समद्विभाजित करती है)
इसलिए, D भुजा AC का मध्य-बिंदु है|
अत: AD = CD ...(i)
(ii) MD || BC दिया है और AC एक तिर्यक रेखा है |
इसलिए ∠ADM = ∠ACB (संगत कोण)
या ∠ADM = 90° [चूँकि ∠ACB = 90°]
अतः MD ⊥ AC है |
(iii) ΔADM तथा ΔCDM में,
AD = CD ... समी० (i) से
MD = MD (उभयनिष्ठ भुजा)
∠ADM = ∠CDM (प्रत्येक 90°)
SAS सर्वांगसमता नियम से,
ΔADM ≌ ΔCDM
इसलिए, MA = CM ...(ii) CPCT नियम से
अब MA + MB = AB
⇒ MA + MA = AB [चूँकि MA = MB]
⇒ 2 MA = AB
⇒ MA = ½ AB
⇒ CM = MA = ½ AB ...समी० (ii) से