Class 9 Maths Chapter 6 Lines and Angles Exercise 6.2 NCERT Solutions in Hindi Medium

रेखाएँ और कोण Ganit NCERT Solutions in Hindi Medium Exercise 6.2
प्रश्न 1. आकृति 6.28 में, x और y के मान ज्ञात कीजिए और फिर दर्शाइए कि AB || CD है।
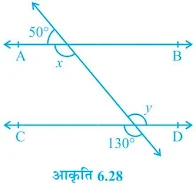
Solution
x + 50° = 180° (रैखिक युग्म)
⇒ x = 180° - 50°
⇒ x = 130°
y = 130°
x = y = 130° (एकांतर कोण गुणधर्म से)
अतः AB || CD
प्रश्न 2. आकृति 6.29 में, यदि AB || CD, CD || EF और y : z = 3 : 7 है, तो x का मान ज्ञात कीजिए |

Solution
दिया है,
AB || CD ...(i)
CD || EF ...(ii)
समीकरण (i) तथा (ii) से हम पाते है कि,
AB || EF ...(iii)
∴ x = z ...(iv) एकांतर कोण
अब, y = 3k तथा z = 7k माना
दिया है,
AB || CD
∴ x + y = 180° (एक ही ओर के अंत: कोणों का योग)
अथवा, z + y = 180°
⇒ 7k + 3k = 180°
⇒ 10k = 180°
⇒ k = 18°
∵ x = z (समी० (iv) से)
∴ x = 7k = 7×18° = 126°
प्रश्न 3. आकृति 6.30 में, यदि AB || CD, EF ⊥ CD और ∠GED = 126° है,तो ∠AGE, ∠GEF और ∠FGE ज्ञात कीजिए |
Solution
∵ ∠AGE = ∠GED (एकान्तर अन्तः कोण)
परन्तु, ∠GED = 126°
⇒ ∠AGE = 126° ...(i)
∴ ∠GEF + ∠FED = 126°
⇒ ∠GEF + 90° = 126° (EF ⊥ CD)
⇒ ∠GEF = 36°
तथा, ∠AGE + ∠FGE = 180° (रेखीय युग्म अभिगृहीत)
⇒ 126° + ∠FGE = 180°
⇒ ∠FGE = 54°
प्रश्न 4. आकृति 6.31 में, यदि PQ || ST, ∠PQR = 110° और ∠RST = 130° है, तो ∠QRS ज्ञात कीजिए |
[संकेत: बिंदु R से होकर ST के समांतर एक रेखा खिचिए]
Solution
R से जाने वाली तथा ST के समान्तर एक रेखा खींचते हैं।
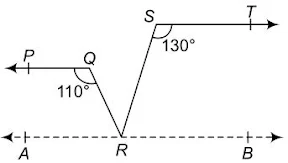
⇒ PQ || ST
तथा, AB || PQ || ST
∵ ∠PQR + ∠QRA = 180° (तिर्यक रेखा के एक ओर के अन्तः कोण)
⇒ 110° + ∠QRA = 180°
⇒ ∠QRA = 70°
∵ ∠TSR = 130° तथा ST || AB
∴ ∠ARS = 130° (एकान्तर अन्तः कोण)
∵ ∠ARS = ∠ARQ + ∠QRS
130° = 70° + ∠QRS
⇒ ∠QRS = 130° - 70° = 60°
⇒ ∠QRS = 60°
प्रश्न 5. आकृति 6.32 में, यदि AB || CD, ∠APQ = 50° और ∠PRD = 127° है ,तो x और Y ज्ञात कीजिए |
Solution
दिया है, AB || CD
⇒ ∠APQ = ∠PQR (एकान्तर अन्तः कोण)
⇒ 50° = x
अब, ∠PQR + ∠QPR = 127°
(एक त्रिभुज का बाह्य कोण अन्तः सम्मुख कोणों के योग के बराबर होता है)
⇒ 50° + ∠QPR = 127°
⇒ y = 77°
प्रश्न 6. आकृति 6.33 में, PQ और RS दो है जो एक दूसरे के सामान्तर रखे गए है | या आपतन किरण (incident ray) AB, दर्पण PQ से B पर टकराती है और प्रवार्तित किरण (reflected ray) पथ BC पर टकराती है तथा पुनः CD के अनुदिश प्रवार्तित हो जाती है | सिद्ध कीजिए कि AB || CD है |
Solution
दिया है: PQ || RS और AB एक आपतन कोण है, CD एक परावर्तित किरण है |
सिद्ध करना है: AB || CD
रचना: BM ⊥ PQ और CN ⊥ RS खिंचा |

प्रमाण:
BM ⊥ PQ and CN ⊥ RS
∴ BM || CM और BC एक तिर्यक रेखा है |
∴ ∠2 = ∠3 ...(i) (एकांतर अंत:कोण)
जबकि हम जानते है कि आपतन कोण = परावर्तन कोण, जहाँ BM और CN अभिलंब हैं |
∴ ∠1 = ∠2 ...(ii)
इसीप्रकार,
∴ ∠3 = ∠4 ...(iii)
समी० (i) (ii) और (iii) से हम पाते है |
∠1 = ∠ 4 ...(iv)
समी० (i) तथा (iv) को जोड़ने पर,
∠1 + ∠2 = ∠3 + ∠4
∠ABC = ∠ BCD (एकांतर अत: कोण)
इसलिए, AB || CD





