Class 9 Maths Chapter 7 Triangles 7.4 NCERT Solutions in Hindi Medium

त्रिभुज Ganit NCERT Solutions in Hindi Medium Exercise 7.4
प्रश्न 1. दर्शाइए कि समकोण त्रिभुज में कर्ण सबसे लंबी भुजा होती है |
Solution
माना ABC एक समकोण त्रिभुज इस प्रकार है कि ∠ABC = 90°
हम जानते हैं कि,
∠ABC + ∠BCA + ∠CAB = 180° (त्रिभुज के गुण द्वारा)
⇒ 90° + ∠BCA + ∠CAB = 180°
⇒ ∠BCA + ∠CAB = 90°
उपरोक्त से, हम देखते हैं कि ∠BCA तथा ∠CAB न्यून कोण हैं।
⇒ ∠BCA < 90°
तथा, ∠CAB < 90°
⇒ ∠BCA < ∠ABC
तथा, ∠CAB < ∠ABC
AB < AC तथा BC < AC (∵ बड़े कोण की सम्मुख भुजा लम्बी होती है)
अतः कर्ण (AC) सबसे लम्बी भुजा है।
प्रश्न 2. आकृति 7.48 में, ΔABC की भुजाओं AB और AC को क्रमश: बिन्दुओं P तथा Q तक बढाया गया है | साथ ही, ∠PBC < ∠QCB है | दर्शाइए कि AC > AB है |

Solution
हम जानते हैं कि,
∠ACB + ∠QCB = 180° (रेखीय युग्म) ...(i)
तथा, ∠ABC + ∠PBC = 180° (रेखीय युग्म ) ...(ii)

समी (i) तथा (ii) से,
∠ABC + ∠PBC = ∠ACB + ∠QCB ...(iii)
परन्तु, ∠PBC < ∠QCB (दिया है) ...(iv)
समी (iii) तथा (iv) से,
∠ABC > ∠ACB
⇒ AC > AB (∵ बड़े कोण की सम्मुख भुजा लम्बी होती है)
प्रश्न 3. आकृति 7.49 में, ∠B < ∠A और ∠C < ∠D है | दर्शाइए कि AD < BC है |

Solution
दिया है, ∠B < ∠A
तथा, ∠C < ∠D
∴ AO < BO ...(i)
तथा, OD < OC ...(ii) (∵ बड़े कोण की सम्मुख भुजा लम्बी होती है)
समी (i) तथा (ii) को जोड़ने पर,
(AO + OD) < (BO + OC)
AD < BC
प्रश्न 4. AB और CD क्रमश: एक चतुर्भुज ABCD की सबसे छोटी और सबसे बड़ी भुजा हैं (देखिये आकृति 7.50) | दर्शाइए कि ∠A > ∠C और ∠B > ∠D है |
Solution
दिया है: ABCD एक चतुर्भुज है। AB सबसे छोटी भुजा तथा CD सबसे बड़ी भुजा है।
सिद्ध करना है: ∠A> ∠C तथा <B> <D
रचना: A को C से तथा B को D से मिलाते हैं।

प्रमाण: ∆ABC में, हमें दिया है कि AB सबसे छोटी भुजा है।
∴ AB < BC
⇒ ∠5 < ∠1 (∵ सबसे बड़ी भुजा का सम्मुख कोण सबसे बड़ा होता है) ...(i)
∆ADC में, हमें दिया है कि CD सबसे बड़ी भुजा है।
∴ CD > AD
⇒ ∠2 > ∠6 ...(ii) (∵ सबसे बड़ी भुजा का सम्मुख कोण सबसे बड़ा होता है)
समी (i) तथा (ii) को जोड़ने पर,
∠1+∠2 > ∠5+∠6
⇒ ∠A > ∠C
अब ∆ADB में, AB सबसे छोटी भुजा है।
∴ AD > AB
⇒ ∠3 > ∠8 ...(iii) (∵ सबसे बड़ी भुजा का सम्मुख कोण सबसे बड़ा होता है)
∆BCD में, CD सबसे बड़ी भुजा है।
∴ CD > BC
⇒ ∠4 > ∠7 ...(iv) (∵ सबसे बड़ी भुजा का सम्मुख कोण सबसे बड़ा होता है)
समी (iii) तथा (iv) को जोड़ने पर,
(∠3 + ∠4) > (∠8 + ∠7)
⇒ ∠B < ∠D
प्रश्न 5. आकृति 7.51 में PR > PQ है और PS कोण QPR समद्विभाजित करता है | सिद्ध कीजिए कि ∠PSR > ∠PSQ है |
Solution
∆PQR में,
PR > PQ (दिया है)
⇒ ∠PQR > ∠PRQ ...(i) (∵ सबसे बड़ी भुजा का सम्मुख कोण सबसे बड़ा होता है)

अब, ∠a = ∠b ...(ii) (∵ PS, ∠QPR को समद्विभाजित करता है)
समी (i) तथा (ii) को जोड़ने पर,
(∠PQR + ∠a) > (∠PRQ + ∠b) ...(iii)
अब, ∠PQS + ∠a + ∠PSQ = 180° (त्रिभुज के गुण द्वारा ) ...(iv)
तथा, ∠PRS + ∠b + ∠PSR = 180° (त्रिभुज के गुण द्वारा ) ...(v)
समी (iv) तथा (v) से,
∠PQS + ∠a + ∠PSQ = ∠PRS + ∠b + ∠PSR = 180°
⇒ ∠PQR + ∠a + ∠PSQ = ∠PRQ + b + ∠PSR ...(vi) (∵ ∠PRS = ∠PRQ, ∠PQS = ∠PQR)
समी (ii) तथा (vi) से,
∠PSQ < ∠PSR (∵ सबसे बड़े कोण की सम्मुख भुजा सबसे लम्बी होती है)
प्रश्न 6. दर्शाइए कि एक रेखा पर एक दिए हुए बिंदु से, जो उस रेखा पर स्थित नहीं है, जितने रेखाखंड खींचे जा सकते हैं उनमें लम्ब रेखाखंड सबसे छोटा होता है।
Solution
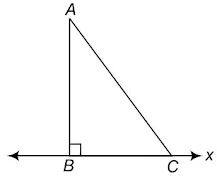
दिया है: x एक रेखा है तथा A एक बिन्दु है जो रेखा x पर स्थित नहीं है। AB ⊥ x, C बिन्दु B को छोड़कर x पर कोई अन्य बिन्दु है।
सिद्ध करना है: AB < AC
प्रमाण:
∆ABC में, ∠B एक समकोण है।
∴ ∠C एक न्यून कोण है।
∴ ∠B > ∠C
⇒ AC > AB (∵ सबसे बड़े कोण की सम्मुख भुजा सबसे लम्बी होती है)
⇒ AB < AC
अतः लम्बवत् रेखाखण्ड सबसे छोटा होता है।



