Class 9 Maths Chapter 13 पृष्ठीय क्षेत्रफल एवं आयतन 13.1 NCERT Solutions in Hindi Medium

पृष्ठीय क्षेत्रफल एवं आयतन Ganit NCERT Solutions in Hindi Medium Exercise 13.1
प्रश्न 1. 1.5 मी लंबा, 1.25 मी चौड़ा और 65 cm गहरा प्लास्टिक का एक डिब्बा बनाया जाना है। इसे ऊपर से खुला रखना है। प्लास्टिक शीट की मोटाई को नगण्य मानते हुए, निर्धरित कीजिएः
(i) डिब्बा बनाने के लिए आवश्यक प्लास्टिक शीट का क्षेत्रफल।
(ii) इस शीट का मूल्य, यदि 1 मी2 शीट का मूल्य 20 रुपए है।
Solution
हम एक प्लास्टिक का डिब्बा रखते हैं, जिसमें
लम्बाई = 1 = 1.5 मी
चौड़ाई = b = 1.25 मी
ऊँचाई = h = 65 सेमी
= 65/100 मी = 0.65 मी (∵1 मी = 100 सेमी)
डिब्बे का वक्रपृष्ठीय क्षेत्रफल = 2 (lb+ bh + hl)
= 2 ( 1.5×1.25 + 1.25×0.65 + 0.65×1.5)
= 2(1.875 + 0.8125 + 0.975)
= 2 (3.6625)
= 7.325 मी2
(i) डिब्बा बनाने के लिए, आवश्यक प्लास्टिक शीट का क्षेत्रफल
= 7.325 - 1×b (∵ डिब्बे का ऊपरी सिरा खुला)
= 7.325 - 1.5×1.25
= 7.325 - 1.875
= 5.45 मी2
(ii) 1 मी2 शीट का मूल्य = ₹20
∴ 5.45 मी2 शीट का मूल्य = ₹ 20×5.45 = ₹109
प्रश्न 2. एक कमरे की लंबाई, चौड़ाई और ऊँचाई क्रमशः 5 मी, 4 मी और 3 मी हैं। 7.50 रुपए प्रति मी2 की दर से इस कमरे की दीवारों और छत पर सफेदी कराने का व्यय ज्ञात कीजिए।
Solution
हम एक कमरा रखते हैं, जिसमें
लम्बाई = 1 = 5 मी
चौड़ाई = b = 4 मी
तथा ऊँचाई = h = 3 मी
सफेदी कराने के लिए अभीष्ट क्षेत्रफल = चार दीवारों का क्षेत्रफल + छत का क्षेत्रफल
= 2 (l + b)×h + (1×b)
= 2(5+4)×3+ (5×4)
= 2×9×3 + 20
= 54+ 20
= 74 मी2
1 मी2 की दर से सफेदी कराने का व्यय = ₹ 7.50
74 मी2 की दर से सफेदी कराने का व्यय = ₹ 7.50×74 = ₹ 555
प्रश्न 3. किसी आयताकार हॉल के फर्श का परिमाप 250 मी है। यदि 10 रुपए प्रति मी2 की दर से चारों दीवारों पर पेंट कराने की लागत 15000 रुपए है, तो इस हॉल की ऊँचाई ज्ञात कीजिए।
[संकेत: चारों दीवारों का क्षेत्रफल = पार्श्व पृष्ठीय क्षेत्रफल]
Solution
माना आयताकार हॉल की लम्बाई = l,
चौड़ाई = b
तथा ऊँचाई = h

हम रखते हैं, हॉल का परिमाप = 2(1 + b) = 250 मी
∵ चार दीवारों का क्षेत्रफल = 1500 मी2 (दिया है)
∴ 2 (l + b)×h = 1500
⇒ 250×h = 1500
⇒ h = 1500/250
⇒ h = 6 मी
अतः हॉल की ऊँचाई 6 मी है।
प्रश्न 4. किसी डिब्बे में भरा हुआ पेंट 9.375 मी2 के क्षेत्रफल पर पेंट करने के लिए पर्याप्त है। इस डिब्बे के पेंट से 22.5 cm × 10 cm × 7.5 cm विमाओं वाली कितनी ईंट पेंट की जा सकती हैं ?
Solution
दिया है, ईंट की विमाएँ,
l = 22.5 सेमी, b = 10 सेमी तथा h = 7.5 सेमी
ईंट का सम्पूर्ण पृष्ठीय क्षेत्रफल = 2 (l×b + b×h + h×l)
= 2 (22.5×10 + 10×7.5 + 7.5×22.5)
= 2(225 + 75+ 168.75)
= 2 × 468.75 सेमी2
= 937.5 सेमी2
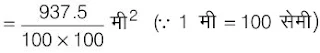
इस डिब्बे के पेन्ट से पेन्ट की जाने वाली ईंटों की संख्या

प्रश्न 5. एक घनाकार डिब्बे का एक किनारा 10 cm लंबाई का है तथा एक अन्य घनाभाकार डिब्बे की लम्बाई, चौड़ाई और ऊँचाई क्रमशः 12.5 cm, 10 cm और 8 cm हैं।
(i) किस डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल अधिक है और कितना अधिक है?
(ii) किस डिब्बे का कुल पृष्ठीय क्षेत्रफल कम है और कितना कम है?
Solution
हम रखते हैं, किसी घनाकार डिब्बे के एक किनारे की लम्बाई l1 = 10 सेमी
तथा किसी अन्य घनाकार डिब्बे के लिए, 1 = 12.5 सेमी
b = 10 सेमी तथा h = 8 सेमी
(i) घनाकार डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल = 4l2
= 4(10)2
= 4×100
= 400 सेमी2
घनाभाकार डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल = 4 (l + b)×h
= 2(12.5+10) × 8
= 2 (22.5)×8
= 45 × 8
= 360 सेमी2
(∵ घनाकार डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल) > (घनाभाकार डिब्बे का पार्श्व पृष्ठीय क्षेत्रफल) (∵ 400 > 360)
∴ अभीष्ट क्षेत्रफल = (400 - 360 ) सेमी2 = 40 सेमी2
(ii) घनाकार डिब्बे का सम्पूर्ण पृष्ठ क्षेत्रफल = 6l2
= 6 (10)2
= 6×100
= 600 सेमी2
घनाभाकार डिब्बे का सम्पूर्ण पृष्ठ क्षेत्रफल = 2 (l×b + b×h + h×1)
= 2 (12.5×10 + 10×8 + 8×12.5)
= 2(125 + 80 + 100)
= 2×305
= 610 सेमी2
∴ (घनाभाकार डिब्बे का क्षेत्रफल) > ( घनाकार डिब्बे का क्षेत्रफल) (∵ 610 > 600)
∴ अभीष्ट क्षेत्रफल = (610 – 600 ) सेमी2 = 10 सेमी2
प्रश्न 6. एक छोटा पौध घर (green house) सम्पूर्ण रूप से शीशे की पट्टियों से (आधर भी सम्मिलित है) घर के अंदर ही बनाया गया है और शीशे की पट्टियों को टेप द्वारा चिपका कर रोका गया है। यह पौधा घर 30 cm लंबा, 25 cm चौड़ा और 25 cm ऊँचा है।
(i) इसमें प्रयुक्त शीशे की पट्टियों का क्षेत्रफल क्या है?
(ii) सभी 12 किनारों के लिए कितने टेप की आवश्यकता है?
Solution
दिया है, पौधे घर की विमाएँ,
l = 30 सेमी, b = 25 सेमी तथा h = 25 सेमी
शीशे का क्षेत्रफल = 2 (l×b + b×h + h×l)
= 2 (30×25 + 25×25 + 25×30)
= 2 (750 + 625 + 750)
= 2 (2125)
= 4250 सेमी2
∴ टेप की लम्बाई = 4 (l + b + h)
= 4 (30+25+25)
[∵ पौधा घर घनाभाकार लम्बाई के आकार का है = 4(l + b + h)]
= 4×80
= 320 सेमी
प्रश्न 7. शांति स्वीट स्टाल अपनी मिठाइयों को पैक करने के लिए गत्ते के डिब्बे बनाने का ऑर्डर दे रहा था। दो मापों के डिब्बों की आवश्यकता थी। बड़े डिब्बों की माप 25 cm × 20 cm × 5 cm और छोटे डिब्बों की माप 15 cm × 12 cm × 5 cm थीं। सभी प्रकार की अतिव्यापिकता (overlaps) के लिए कुल पृष्ठीय क्षेत्रफल के 5% के बराबर अतिरिक्त गत्ता लगेगा। यदि गत्ते की लागत 4 रुपए प्रति 1000 सेमी2 है, तो प्रत्येक प्रकार के 250 डिब्बे बनवाने की कितनी लागत आएगी?
Solution
बड़े डिब्बे की विमाएँ हैं, 1 = 25 सेमी, b = 20 सेमी तथा h = 5 सेमी
बड़े आकार के डिब्बे का सम्पूर्ण पृष्ठीय क्षेत्रफल
= 2 (l×b + b×h + h×l)
= 2 (25×20 + 20×5 + 5×25)
= 2(500 + 100 + 125)
= 2 (725)
= 1450 सेमी2
छोटे डिब्बे के लिए विमाएँ,
= 15 सेमी, b = 12 सेमी तथा h = 5 सेमी
छोटे आकार के डिब्बे का सम्पूर्ण पृष्ठ क्षेत्रफल
= 2 (15×12 + 12×5 + 5×15)
= 2 (180 + 60 + 75)
= 2 (315)
= 630 सेमी2
सभी अतिव्यापिकता के लिए क्षेत्रफल
दोनों डिब्बों का तथा अतिव्यापिकता का सम्पूर्ण पृष्ठ क्षेत्रफल
= (2080 + 104)
= 2184 सेमी2
250 डिब्बों के लिए सम्पूर्ण पृष्ठ क्षेत्रफल
= 2184 × 250 सेमी2
1000 सेमी2 के लिए गत्ते का व्यय = ₹ 4
प्रश्न 8. परवीन अपनी कार खड़ी करने के लिए, एक संदूक के प्रकार के ढाँचे जैसा एक अस्थाई स्थान तिरपाल की सहायता से बनाना चाहती है, जो कार को चारों ओर से और ऊपर से ढक ले (सामने वाला फलक लटका हुआ होगा जिसे घुमाकर ऊपर किया जा सकता है)। यह मानते हुए कि सिलाई के समय लगा तिरपाल का अतिरिक्त कपड़ा नगण्य होगा, आधार विमाओं 4 मीटर × 3 मीटर और ऊँचाई 2.5 मीटर वाले इस ढाँचे को बनाने के लिए कितने तिरपाल की आवश्यकता होगी?
Solution
ढाँचे के लिए विमाएँ हैं, l = 4 मी, b = 3 मी तथा h = 2.5 मी
ढाँचे को बनाने के लिए तिरपाल का अभीष्ट क्षेत्रफल
= कार की (4 भुजाओं का क्षेत्रफल + ऊपरी भाग का क्षेत्रफल)
= 2 (l + b)×h + (l × b)
= 2(4 + 3)×2.5 + (4×3)
= (2×7×2.5) + 12
= 35 + 12
= 47 मी2


