Class 9 Maths Chapter 11 Constructions 11.1 NCERT Solutions in Hindi Medium

रचनाएँ Ganit NCERT Solutions in Hindi Medium Exercise 11.1
प्रश्न 1. एक दी हुई किरण के प्रारम्भिक बिन्दु पर 90° के कोण की रचना कीजिए और कारण सहित रचना की पुष्टि कीजिए ।
Solution
रचना के चरण:

- O को केन्द्र मानकर तथा कोई त्रिज्या लेकर एक चाप लगाइए जो किरण OA को बिन्दु B पर प्रतिच्छेद करता है।
- B को केन्द्र मानकर और उसी त्रिज्या, जो पहले ली गयी थी, से एक चाप खींचते हैं, जो चरण (1) में खींचे गए चाप को बिन्दु C पर प्रतिच्छेद करता है।
- C को केन्द्र मानकर और उसी त्रिज्या, जो पहले ली गयी थी, से एक चाप खींचते हैं, जो चरण (1) में खींचे गए चाप को बिन्दु D पर प्रतिच्छेद करता है।
- C से जाने वाली किरण OE खींचते हैं।
तब, ∠EOA = 60° - D से जाने वाली किरण OF खींचते हैं।
तब, ∠FOE = 60° - पुन: C तथा D को केन्द्र मानकर तथा ½ CD से बड़ी त्रिज्या लेकर चाप लगाइए, एक-दूसरे को G पर प्रतिच्छेद करते है।
- किरण OG खींचते हैं। यह किरण OG, ZFOE का समद्विभाजक होती है। अर्थात्
अतः ∠GOA = ∠GOE + ∠EOA = 30° + 60° = 90°
औचित्य प्रतिपादन
(i) BC को मिलाते हैं।
तब, OC = OB = BC (रचना से)
∴ ∆COB एक समबाहु त्रिभुज है।
∴ ∠COB = 60°
∴ ∠EOA = 60°
(ii) CD को मिलाते हैं।
तब, OD = OC = CD (रचना से)
∴ ∆DOC एक समबाहु त्रिभुज है।
∴ ∠DOC = 60°
∴ ∠FOE = 60°
(iii) CG तथा DG को मिलाते हैं।
∆ODG तथा ∆OCG में,
OD = OC (एक ही चाप की त्रिज्या)
DG = CG (एक ही चाप की त्रिज्या)
OG = OG (उभयनिष्ठ)
∆ODG ≅ ∆OCG (SSS नियम द्वारा)
∴ ∠DOG = ∠COG (CPCT द्वारा)
अत: ∠GOA = ∠GOE + ∠EOA = 30° + 60° = 90°
प्रश्न 2. एक दी हुई किरण के प्रारम्भिक बिन्दु पर 45° के कोण की रचना कीजिए और कारण सहित रचना की पुष्टि कीजिए ।
Solution
रचना के चरण:

- O को केन्द्र मानकर तथा कोई त्रिज्या लेकर एक चाप लगाइए जो किरण OA को बिन्दु B पर प्रतिच्छेद करता है।
- B को केन्द्र मानकर और उसी त्रिज्या, जो पहले ली गयी थी, से एक चाप खींचते हैं, जो चरण (1) में खींचे गए चाप को बिन्दु C पर प्रतिच्छेद करता है।
- C को केन्द्र मानकर और उसी त्रिज्या, जो पहले ली गयी थी, से एक चाप खींचते हैं, जो चरण (1) में खींचे गए चाप को बिन्दु D पर प्रतिच्छेद करता है।
- C से जाने वाली किरण OE खींचते हैं। तब, ∠EOA = 60°
- D से जाने वाली किरण OF खींचते हैं। तब, ∠FOE = 60°
- पुनः C तथा D को केन्द्र मानकर तथा ½CD से बड़ी त्रिज्या लेकर चाप लगाइए जो एक-दूसरे को G पर प्रतिच्छेद करते हैं।
- किरण OG खींचते हैं। यह किरण OG, ∠FOE का समद्विभाजक होती है अर्थात्
अतः ∠GOA = ∠GOE + ∠EOA = 30° + 60° = 90° - अब, O को केन्द्र मानकर तथा कोई त्रिज्या लेकर एक चाप लगाइए जो किरण OA तथा OG को बिन्दुओं क्रमशः H तथा I पर प्रतिच्छेद करता है।
- पुन: H तथा I को केन्द्र मानकर तथा ½HI से बड़ी त्रिज्या लेकर चाप लगाइए, जो माना एक-दूसरे को J पर प्रतिच्छेद करता है।
- किरण OJ खींचते हैं। यह किरण, OJ, ∠GOA का समद्विभाजक होती है। अर्थात्
औचित्य प्रतिपादन:
(i) BC को मिलाइए
तब, OC = OB = BC (रचना से)
∴ ∆COB एक समबाहु त्रिभुज है।
∴ ∠COB = 60°
∴ ∠EOA = 60°
(ii) CD को मिलाइए
तब, OD = OC = CD (रचना से)
∴ ∆DOC एक समबाहु त्रिभुज है।
∴ ∠DOC = 60°
∴ ∠FOE = 60°
(iii) CG तथा DG को मिलाते हैं।
∆ODG तथा ∆OCG में,
OD = OC (एक ही चाप की त्रिज्याएँ)
DG = CG (एक ही त्रिज्या के चाप)
OG = OG (उभयनिष्ठ)
∴ ∆ODG ≌ ∆OCG (SSS नियम)
∴ ∠DOG = ∠COG (CPCT द्वारा)

अतः ∠GOA = ∠GOE + ∠EOA = 30° + 60° = 90°
(iv) HJ तथा IJ को मिलाते हैं।
∆OIJ तथा ∆OHJ में,
OI = OH (एक ही चाप की त्रिज्याएँ)
IJ = HJ (एक ही त्रिज्याओं के चाप)
OJ = OJ (उभयनिष्ठ)
∴ ∆OIJ ≌ ∆OHJ (SSS नियम)
∴ ∠IOJ = ∠HOJ (CPCT द्वारा)

प्रश्न 3. निम्न मापों के कोणों की रचना कीजिए ।
(i) 30°
(ii) 22½°
(iii) 15°
Solution
(i) रचना के चरण:

- O को केन्द्र मानकर तथा कोई त्रिज्या लेकर एक चाप लगाइए जो किरण OA को बिन्दु B पर प्रतिच्छेद करता है।
- B को केन्द्र मानकर और उसी त्रिज्या, जो पहले ली गयी थी, से एक चाप खींचते हैं, जो चरण (1) में खींचे गए चाप को बिन्दु C पर प्रतिच्छेद करता है।
- C से जाने वाली किरण OF खींचते हैं।
तब, ∠EOA = 60° - पुनः B तथा C को केन्द्र मानकर तथा ½ BC से बड़ी त्रिज्या लेकर चाप लगाइए, जो एक-दूसरे को D पर प्रतिच्छेद करते हैं।
- किरण OD खींचते हैं, यह किरण OJ, ∠EOA का समद्विभाजक होती है।
अर्थात् ∠EOD = ∠AOD = ½∠EOA = ½(60°) = 30°
(ii) रचना के चरण:

- O को केन्द्र मानकर तथा कोई त्रिज्या लेकर एक चाप लगाइए जो किरण OA को बिन्दु B पर प्रतिच्छेद करता है।
- B को केन्द्र मानकर और उसी त्रिज्या, जो पहले ली गयी थी, से एक चाप खींचते हैं, जो चरण (1) में खींचे गए चाप को बिन्दु C पर प्रतिच्छेद करता है।
- C को केन्द्र मानकर और उसी त्रिज्या, जो पहले ली गयी थी, से एक चाप खींचते हैं, जो चरण (1) में खींचे गए चाप को बिन्दु D पर प्रतिच्छेद करता है।
- C से जाने वाली किरण OF खींचते हैं। तब, ∠EOA = 60°
- D से जाने वाली किरण OF खींचते हैं। तब, ∠FOE = 60°
- पुनः C तथा D को केन्द्र मानकर तथा 1 CD से बड़ी त्रिज्या लेकर चाप लगाइए, जो एक-दूसरे को G पर प्रतिच्छेद करते हैं।
- किरण OG खींचते हैं। यह किरण OG, ∠FOE का समद्विभाजक होती है अर्थात्
अतः ∠GOA = ∠GOE + ∠EOA = 30° + 60° = 90° - अब, O को केन्द्र मानकर तथा कोई त्रिज्या लेकर एक चाप लगाइए, जो किरण OA तथा OG को बिन्दुओं क्रमश: H तथा I पर प्रतिच्छेद करता है।
- पुन: H तथा I को केन्द्र मानकर तथा ½ HI से बड़ी त्रिज्या लेकर चाप लगाइए, जो एक-दूसरे को J पर प्रतिच्छेद करते हैं।
- किरण OJ खींचते हैं। यह किरण, OJ, ∠GOA का समद्विभाजक होती है। अर्थात्
- पुन: O को केन्द्र मानकर तथा कोई त्रिज्या लेकर एक चाप लगाइए, जो किरण OA तथा OJ को बिन्दुओं क्रमश: K तथा L पर प्रतिच्छेद करता है।
- पुनः K तथा L को केन्द्र मानकर तथा ½ KL से बड़ी त्रिज्या लेकर चाप लगाइए, जो एक-दूसरे को H पर प्रतिच्छेद करते हैं।
- किरण OM खींचते हैं। यह किरण OM, ∠AOJ का समद्विभाजक होती है। अर्थात्
∠JOM = ∠AOM
(iii) रचना के चरण:
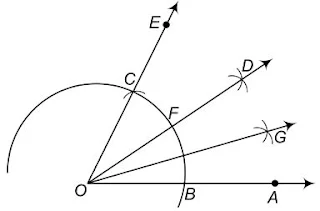
- O को केन्द्र मानकर तथा कोई त्रिज्या लेकर एक चाप लगाइए, जो किरण OA को बिन्दु B पर प्रतिच्छेद करता है।
- B को केन्द्र मानकर और उसी त्रिज्या, जो पहले ली गयी थी, से एक चाप खींचते हैं, जो चरण (1) में खींचे गए चाप को बिन्दु C पर प्रतिच्छेद करता है।
- C से जाने वाली किरण OE खींचते हैं। तब, ∠EOA = 60°
- अब, B तथा C को केन्द्र मानकर तथा ½BC से बड़ी त्रिज्या लेकर चाप लगाइए, जो एक-दूसरे को D पर प्रतिच्छेद करते हैं।
- किरण OD खींचते हैं, जो चरण (1) में खींचे गए चाप को बिन्दु F पर प्रतिच्छेद करता है। यह किरण OD, ∠EOA का समद्विभाजक होती है, अर्थात् ∠EOD = ∠AOD = ½ ∠EOA = ½ (60°) = 30°
- अब, B तथा F को केन्द्र मानकर तथा ½ BF से बड़ी त्रिज्या लेकर चाप लगाइए, जो एक-दूसरे को G पर प्रतिच्छेद करते हैं।
- किरण OG खींचते हैं। यह किरण OG, ∠AOD का समद्विभाजक होती है अर्थात्
प्रश्न 4. निम्न कोणों की रचना कीजिए और चाँदे द्वारा मापकर पुष्टि कीजिए।
(i) 75°
(ii) 105°
(iii) 135°
Solution
(i) रचना के चरण:

- O को केन्द्र मानकर तथा कोई त्रिज्या लेकर एक चाप लगाइए, जो किरण OA को बिन्दु B पर प्रतिच्छेद करता है।
- B को केन्द्र मानकर और उसी त्रिज्या, जो पहले ली गयी थी, से एक चाप खींचते हैं, जो चरण (1) में खींचे गए चाप को बिन्दु C पर प्रतिच्छेद करता है।
- C को केन्द्र मानकर और उसी त्रिज्या, जो पहले ली गयी थी, से एक चाप खींचते हैं, जो चरण (1) में खींचे गए चाप को बिन्दु D पर प्रतिच्छेद करता है।
- C से जाने वाली किरण OF खींचते हैं।
तब, ∠EOA = 60° - D से जाने वाली किरण OF खींचते हैं।
तब, ∠FOE = 60° - पुन: C तथा D को केन्द्र मानकर तथा ½ CD से बड़ी त्रिज्या लेकर चाप लगाइए, जो एक-दूसरे को G पर प्रतिच्छेद करते हैं।
- किरण OG को खींचिए, जो चरण (1) में खींचे गए चाप को बिन्दु H पर प्रतिच्छेद करता है। यह किरण OG, ∠FOE का समद्विभाजक होती है। अर्थात्
- पुनः C तथा H को केन्द्र मानकर तथा ½ CH से बड़ी त्रिज्या लेकर चाप लगाइए, जो एक-दूसरे को I पर प्रतिच्छेद करते हैं।
- किरण OI को खींचिए, यह किरण OI, ∠GOE का समद्विभाजक होती है।
अर्थात् ∠GOI = ∠EOI = ½∠GOE = ½(30°) = 15°
अतः ∠IOA = ∠IOE + ∠EOA = 15° + 60° = 75°
परकार से ∠IOA को मापने पर, हम प्राप्त करते हैं कि ∠IOA = 15°,
अतः रचना सही है।

- O को केन्द्र मानकर तथा कोई त्रिज्या लेकर एक चाप लगाइए, जो किरण OA को बिन्दु B पर प्रतिच्छेद करता है।
- B को केन्द्र मानकर और उसी त्रिज्या, जो पहले ली गयी थी, से एक चाप खींचते हैं, जो चरण (1) में खींचे गए चाप को बिन्दु C पर प्रतिच्छेद करता है।
- C को केन्द्र मानकर और उसी त्रिज्या, जो पहले ली गयी थी, से एक चाप खींचते हैं, जो चरण (1) में खींचे गए चाप को बिन्दु D पर प्रतिच्छेद करता है।
- C से जाने वाली किरण OF खींचते हैं।
तब, ∠EOA = 60° - D से जाने वाली किरण OF खींचते हैं।
तब, ∠FOE = 60° - पुनः C तथा D को केन्द्र मानकर तथा ½ CD से बड़ी त्रिज्या लेकर चाप लगाइए, जो एक-दूसरे को G पर प्रतिच्छेद करते हैं।
- किरण OG को खींचिए, जो चरण (1) में खींचे गए चाप को बिन्दु H पर प्रतिच्छेद करता है, यह किरण OG, ∠FOE का समद्विभाजक होती है। अर्थात्
अतः ∠GOA = ∠GOE + ∠EOA = 30° + 60° = 90° - पुनः H तथा D को केन्द्र मानकर तथा ½ HD से बड़ी त्रिज्या लेकर चाप लगाइए, जो एक-दूसरे को I पर प्रतिच्छेद करते हैं।
- किरण OI खींचिए| यह किरण OI, ∠FOG का समद्विभाजक है अर्थात्
∠FOI = ∠GOI = ½ ∠FOG = ½ (30°) = 15°
अतः ∠IOA = ∠IOG + ∠GOA = 15° + 90° = 105°
परकार से ∠IOA का मापन करने पर, हम प्राप्त करते हैं, ∠FOA = 105°
अतः रचना की पुष्टि हो चुकी है।
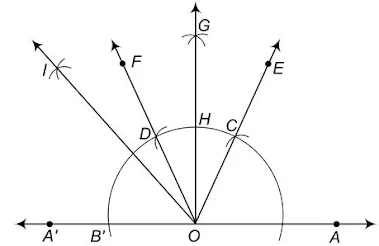
- किरण OA' निरूपित करने के लिए AO को A' तक बढ़ाते हैं।
- O को केन्द्र मानकर तथा कोई त्रिज्या लेकर एक चाप लगाइए, जो किरण OA को बिन्दु B पर तथा OA' को बिन्दु B' पर प्रतिच्छेद करता है।
- B को केन्द्र मानकर और उसी त्रिज्या, जो पहले ली गयी थी, से एक चाप खींचते हैं, जो चरण (1) में खींचे गए चाप को बिन्दु C पर प्रतिच्छेद करता है।
- C को केन्द्र मानकर और उसी त्रिज्या, जो पहले ली गयी थी, से एक चाप खींचते हैं, जो चरण (1) में खींचे गए चाप को बिन्दु D पर प्रतिच्छेद करता है।
- C से जाने वाली किरण OF खींचते हैं। तब, ∠EOA = 60°
- D से जाने वाली किरण OF खींचते हैं। तब, ∠FOE = 60°
- पुनः C तथा D को केन्द्र मानकर तथा ½ CD से बड़ी त्रिज्या लेकर चाप लगाइए, जो एक-दूसरे को G पर प्रतिच्छेद करते हैं।
- किरण OG खींचते हैं। यह किरण OG, ∠FOE का समद्विभाजक होती है। अर्थात्
अतः ∠GOA = ∠GOE + ∠EOA = 30° + 60° = 90°
∴ ∠B′OH = 90° - पुनः B' तथा H को केन्द्र मानकर तथा ½ B'H से बड़ी त्रिज्या लेकर चाप लगाइए, जो एक-दूसरे को I/ पर प्रतिच्छेद करते हैं।
- किरण OI खींचिए। यह किरण OI, ∠BOG का समद्विभाजक है
अर्थात् ∠B'OI = ∠GOI = ½ ∠B'OG = ½ (90°) = 45°
अतः ∠IOA = ∠IOG + ∠GOA = 45° + 90° = 135°
परकार द्वारा ∠IOA का मापन करने पर, हम प्राप्त करते हैं ∠IOA = 135°
अतः रचना की पुष्टि हो चुकी है।
प्रश्न 5. एक समबाहु त्रिभुज की रचना कीजिए, जब इसकी भुजा दी हो तथा कारण सहित रचना कीजिए।
Solution
रचना के चरण:

- प्रारम्भिक बिन्दु A के साथ एक किरण AX लेते हैं। AX से, AB = 4 सेमी का भाग काटते हैं।
- A को केन्द्र मानकर तथा त्रिज्या (4 सेमी) लेकर वृत्त का एक चाप लगाइए, जो किरण AX को बिन्दु B पर प्रतिच्छेद करता है।
- B को केन्द्र मानकर और उसी त्रिज्या, जो पहले ली गयी थी, से एक चाप खींचते हैं, जो चरण (2) में खींचे गए चाप को बिन्दु C पर प्रतिच्छेद करता है।
- C से जाने वाली किरण AE खींचते हैं।
- पुनः B को केन्द्र मानकर तथा त्रिज्या (4 सेमी) लेकर वृत्त का एक चाप लगाइए, जो किरण AX को बिन्दु A पर प्रतिच्छेद करता है।
- A को केन्द्र मानकर और उसी त्रिज्या, जो चरण (5) में ली गयी थी, से वृत्त का एक चाप खींचते हैं, जो चरण (3) में खींचे गए चाप को बिन्दु C पर प्रतिच्छेद करता है।
- C से जाने वाली किरण BF खींचते हैं। तब, अभीष्ट ∆ABC है, जो 4 सेमी की भुजा देता है।
AB = BC (रचना से)
AB = AC (रचना से)
∴ AB = BC = (CA)
∴ ∆ABC एक समबाहु त्रिभुज है।
∴ रचना की पुष्टि हो चुकी है।





