Class 9 Maths Chapter 10 Circles 10.4 NCERT Solutions in Hindi Medium

वृत्त Ganit NCERT Solutions in Hindi Medium Exercise 10.4
प्रश्न 1. 5 cm तथा 3 cm त्रिज्या वाले दो वृत्त दो बिन्दुओं पर प्रतिच्छेद करते हैं तथा उनके केन्द्रों बीच की दूरी 4 cm है। उभयनिष्ठ जीवा की लम्बाई ज्ञात कीजिए।
Solution
त्रिज्या 5 सेमी तथा 3 सेमी के वृत्तों के केन्द्र क्रमशः O तथा O' हैं।
माना AB इनकी उभयनिष्ठ जीवा है।

दिया है,
OA = 5 सेमी, O 'A = 3 सेमी तथा OO' = 4 सेमी
∴AO'2 + OO'2
= 32 + 42
= 9+16
=25
= OA2
इसलिए OO'A, समकोण त्रिभुज है जो O पर समकोण है।

समी (i) तथा (ii) से,
2 AM = 6
⇒ AM = 3
चूँकि जब दो वृत्त दो बिन्दुओं पर प्रतिच्छेद करते हैं, तब इनके केन्द्र उभयनिष्ठ जीवा के लम्बार्द्धक पर स्थित होते हैं।
AB = 2×AM = 2×3 = 6 सेमी
प्रश्न 2. यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें, तो सिद्ध कीजिए कि एक जीवा के खंड दूसरी जीवा के संगत खंडों के बराबर हैं।
Solution
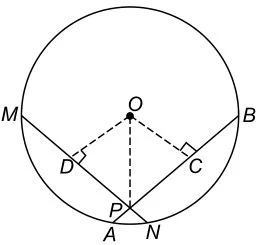
दिया है: केन्द्र O के साथ एक वृत्त की दो जीवाएँ MN तथा AB हैं, MN तथा AB बिन्दु P पर प्रतिच्छेद करती हैं तथा MN = AB
सिद्ध करना है: MP = PB तथा PN = AP
रचना: OD ⟂ MN तथा OC ⟂ AB खींचिए। OP को मिलाइए।
प्रमाण:
∵ DM = DN
= ½ MN (केन्द्र से लम्ब जीवा को समद्विभाजित करता है)
तथा, AC = CB = ½ AB (केन्द्र से लम्ब जीवा को समद्विभाजित करता है)
MD = BC तथा DN = AC (∵ MN = AB) ...(i)
∆ODP तथा ∆OPC में,
OD = OC (वृत्त की समान जीवाएँ केन्द्र से समदूरस्थ होती हैं)
∠ODP = ∠OCP
OP = OP (उभयनिष्ठ)
सर्वांगसम की RHS युक्ति से,
∆ODP ≌ ∆OCP
∴ DP = PC (CPCT द्वारा ) ...(ii)
समी (i) तथा (ii) को जोड़ने पर,
MD + DP = BC + PC
MP = PB
समी (i) में से समी (ii) को घटाने पर,
DN – DP = AC – PC
PN = AP
अत: MP = PB तथा PN = AP
प्रश्न 3. यदि एक वृत्त की दो समान जीवाएँ वृत्त के अन्दर प्रतिच्छेद करें, तो सिद्ध कीजिए कि प्रतिच्छेद बिन्दु को केंद्र से मिलाने वाली रेखा जीवाओं से बराबर कोण बनाती है।
Solution
दिया है: केन्द्र O के साथ एक वृत्त की जीवाएँ RQ तथा MN हैं। MN तथा RQ बिन्दु पर प्रतिच्छेद करती है तथा MN = RQ
सिद्ध करना है: ∠OPC = ∠OPB
रचना: OC ⟂ RQ तथा OB ⟂ MN खींचते हैं। OP को मिलाने पर।

प्रमाण:
∆OCP तथा ∆OBP में,
∠OCP = ∠OBP (प्रत्येक = 90°)
OP = OP (उभयनिष्ठ)
OC = OB (एक वृत्त की समान जीवाएँ केन्द्र से समदूरस्थ होती हैं)
सर्वांगसम की RHS युक्ति से,
∆OCP ≌ ∆OBP
∠OPC = ∠OPB (CPCT द्वारा)
प्रश्न 4. यदि एक रेखा दो संकेंद्री वृतों (एक ही केंद्र वाले वृत्त) को, जिनका केंद्र O है, A, B, C और D पर प्रतिच्छेद करे, तो सिद्ध कीजिए AB = CD है | (देखिए आकृति 10.25)

Solution
माना रेखा l पर O से लम्ब OP है। चूँकि एक वृत्त के केन्द्र से जीवा पर डाला गया लम्ब इसे समद्विभाजित करता है।
अब, छोटे वृत्त एक जीवा BC है तथा OP ⟂ BC
∴ BP = PC ...(i)

चूँकि बड़े वृत्त की एक जीवा AD है तथा OP ⟂ AD
∴ AP = PD
समी (ii) में से समी (i) को घटाने पर,
AP – BP = PD – PC
⇒ AB = CD
प्रश्न 5. एक पार्क में बने 5 m त्रिज्या वाले वृत्त पर खड़ी तीन लड़कियाँ रेशमा, सलमा एवं मनदीप खेल रही हैं। रेशमा एक गेंद को सलमा के पास, सलमा मनदीप के पास तथा मनदीप रेशमा के पास फेंकती है। यदि रेशमा तथा सलमा के बीच और सलमा तथा मनदीप के बीच की प्रत्येक दूरी 6 m हो, तो रेशमा और मनदीप के बीच की दूरी क्या है?
Solution
माना वृत्त का केन्द्र O है तथा रेशमा, सलमा और मनदीप वृत्त पर क्रमशः बिन्दुओं R, S तथा M द्वारा प्रदर्शित हैं।
माना RP = x मी

∆ORS का क्षेत्रफल = ½ × x × 5 = 5x/2 ...(i)
(∆ORM में, RM एक जीवा है अत: OP ⊥ RM)
पुन: ∆ORS का क्षेत्रफल = ½ × RS × ON
= ½ × 6 × 4 = 12 ...(ii)
[∵ RS एक जीवा है, अत: ON ⊥ RS
समकोण ∆RON मे, OR2 = RN2 + NO2
⇒ 52 = 32 + NO2
⇒ NO2 = 25 – 9 = 16
⇒ NO = 4 सेमी]
समी (i) तथा (ii) से,
5x/2 = 12
⇒ x = 24/5
चूँकि RM का मध्य- बिन्दु P है |
अतः रेशमा तथा मनदीप के बीच की दूरी 9.6 मी है।
प्रश्न 6. 20 m त्रिज्या का एक गोल पार्क (वृत्ताकार) एक कालोनी में स्थित है। तीन लड़के अंकुर, सैयद तथा डेविड इसकी परिसीमा पर बराबर दूरी पर बैठे हैं और प्रत्येक के हाथ में एक खिलौना टेलीफोन आपस में बात करने के लिए है। प्रत्येक फोन की डोरी की लम्बाई ज्ञात कीजिए।
Solution
माना सैयद्द, अंकुर तथा डेविड बिंदुओं P, Q तथा R पर खड़े हैं।
माना, PQ = QR = PR = x

अतः PQR एक समबाहु त्रिभुज है। त्रिभुज की भुजाओं पर शीर्षों से शीर्षलम्ब PC, QD तथा RN खींचते हैं तथा ये शीर्षलम्ब वृत्त के केंद्र M पर प्रतिच्छेद करते हैं।
चूँकि PQR एक समबाहु त्रिभुज है, अतः ये शीर्षलम्ब इसकी भुजाओं को समद्विभाजित करते हैं।



