Class 9 Maths Chapter 10 Circles 10.5 NCERT Solutions in Hindi Medium

वृत्त Ganit NCERT Solutions in Hindi Medium Exercise 10.5
प्रश्न 1. आकृति 10.36 में, केंद्र O वाले एक वृत्त पर तीन बिंदु A, B और C इस प्रकार हैं कि ∠BOC = 30° तथा ∠AOB = 60° है | यदि चाप ABC के अतिरिक्त वृत्त पर D एक बिंदु है, रो ∠ADC ज्ञात कीजिए |

Solution
∠AOC = 2 ∠ADC
(एक चाप द्वारा केंद्र पर आन्तरित कोण वृत्त के शेष भाग के किसी बिंदु पर आन्तरित कोण का दोगुना होता है)
⇒ ∠AOB + ∠BOC = 2∠ADC
⇒ 60° + 30° = 2 ADC
⇒ 2∠ADC = 90°
⇒ ∠ADC = 90°/2 = 45°
अतः ∠ADC = 45°
प्रश्न 2. किसी वृत्त की एक जीवा वृत्त की त्रिज्या के बराबर है | जीवा द्वारा लघु चाप के किसी बिंदु पर अंतरित कोण ज्ञात कीजिए तथा दीर्घ चाप के किसी बिंदु पर भी अंतरित कोण ज्ञात कीजिए |
Solution

चाप BC त्रिज्याएँ OB तथा OC के बराबर है |
इसलिए ΔBOC एक समबाहु त्रिभुज है |
अत: ∠BOC = 60° (समबाहु त्रिभुज के प्रत्येक कोण)
अब, ∠BOC = 2∠BAC
(एक चाप द्वारा केंद्र पर आन्तरित कोण वृत्त के शेष भाग के किसी बिंदु पर आन्तरित कोण का दोगुना होता है)
⇒ 60° = 2∠BAC
⇒ ∠BAC = 60°/2 = 30°
अतः दिर्घ चाप में बना कोण 30° है |
अब चूँकि BACM एक चक्रीय चतुर्भुज है |
इसलिए, ∠A + ∠M = 180° (चक्रीय चतुर्भुज के सम्मुख कोणों का योग)
⇒ 30° + M = 180°
⇒ ∠M = 180° - 30°
⇒ ∠M = 150°
अतः दीर्घ वृत्त में बना कोण 150° है |
प्रश्न 3. आकृति 10.37 में, ∠PQR = 100° है, जहाँ P, Q तथा R केंद्र O वाले एक वृत्त पर स्थित बिंदु हैं | ∠OPR ज्ञात कीजिए |

Solution
दिया है: ∠PQR = 100° है |
चूँकि वृत्त के केंद्र पर बना कोण शेष वृत्त पर बने कोण का दुगुना होता है, इसलिए
∠POR = 2 ∠PQR
⇒ ∠POR = 2 × 100°
⇒ ∠POR = 200°
अब प्रतिवर्ती, ∠POR = 360° - 200°
⇒ प्रतिवर्ती ∠POR = 160°
ΔPOR में,
PO = RO (एक ही वृत्त की त्रिज्या)
इसलिए ∠OPR = ∠ORP ...(i) (बराबर भुजाओं के सम्मुख कोण बराबर होते हैं)
अब, ∠OPR + ∠ORP + ∠POR = 180° (तीनों कोणों का योग)
⇒ ∠OPR + ∠OPR + 160° = 180° [समी० (i) से]
⇒ 2 ∠OPR = 180° - 160°
⇒ 2 ∠OPR = 20°
⇒ ∠OPR = 20°/2
⇒ ∠OPR = 10°
प्रश्न 4. आकृति 10.38 में, ∠ABC = 69° और ∠ACB = 31° हो, तो ∠BDC ज्ञात कीजिए |
Solution
ΔABC में,
∠ABC + ∠ACB + ∠BAC = 180° (त्रिभुज के तीनों का योग)
⇒ 69° + 31° + ∠BAC = 180°
⇒ 100° + ∠BAC = 180°
⇒ ∠BAC = 180° - 100°
⇒ ∠BAC = 80°
अब चूँकि, ∠BAC = ∠BDC
इसलिए, ∠BDC = 80°
प्रश्न 5. आकृति 10.39 में, एक वृत्त पर A, B, C और D चार बिंदु हैं | AC और BD एक बिंदु E पर इस प्रकार प्रतिच्छेद करते हैं कि ∠BEC = 130° तथा ∠ECD = 20° है | ∠BAC ज्ञात कीजिए |
Solution
BED एक सरल रेखा है |
इसलिए, ∠BEC + ∠CED = 180° (रैखिक युग्म)
⇒ 130° + ∠CED = 180°
⇒ ∠CED = 180° - 130°
⇒ ∠CED = 50°
अब, ∠BAC = ∠CED (क्योंकि एक ही वृत्त खंड में बने कोण बराबर होते हैं)
इसलिए, ∠BAC = 50°
प्रश्न 6. ABCD एक चक्रीय चतुर्भुज है जिसके विकर्ण एक बिन्दु E पर प्रतिच्छेद करते हैं। यदि ∠DBC = 70° और ∠BAC = 30° हो, तो ∠BCD ज्ञात कीजिए। पुनः यदि AB = BC हो, तो ∠ECD ज्ञात कीजिए ।
Solution

दिया है कि ∠DBC = 70° और ∠BAC = 30° है |
अब, ∠BAC = ∠BDC (एक ही वृत्त खंड में बने कोण बराबर होते हैं)
इसलिए, ∠BDC = 30° ...(i)
अब ∆BCD में,
∠BDC = 30°, ∠DBC = 70° और ∠BCD = ?
अब ∠BDC + ∠DBC + ∠BCD = 180° (त्रिभुज के तीनों कोणों का योग)
⇒ 30° + 70° + ∠BCD = 180° [समी० (i) से]
⇒ 100° + ∠BCD = 180°
⇒ ∠BCD = 180° - 100°
⇒ ∠BCD = 80°
अब, AB = BC (दिया है)
इसलिए, ∠BAC = ∠BCA ...(ii) [बराबर भुजाओं के सम्मुख कोण बराबर होते हैं]
अब चूँकि ∠BAC = 30° है |
इसलिए ∠BCA = 30° [समी० (ii) से]
⇒ ∠ECB = 30°
चूँकि ∠BCD = 80°
⇒ ∠ECB + ∠ECD = 80°
⇒ 30° + ∠ECD = 80°
⇒ ∠ECD = 80° - 30°= 50°
अत: ∠ECD = 50° और ∠BCD = 80° है |
प्रश्न 7. यदि एक चक्रीय चतुर्भुज के विकर्ण उसके शीर्षों से जाने वाले वृत्त के व्यास हों, तो सिद्ध कीजिए कि वह एक आयत है।
Solution
दिया है: ABCD एक चक्रीय चतुर्भुज है जिसके विकर्ण AC तथा BD बिंदु O पर प्रतिच्छेद करते हैं।

सिद्ध करना है: NQPM एक आयत है ।
प्रमाण:
ΔNOQ तथा ΔPOM में,
ON = OP (एक ही वृत्त कि त्रिज्यायें)
OQ = OM (एक ही वृत्त कि त्रिज्यायें)
∠NOQ = ∠POM (शिर्षाभिमुख कोण)
SAS सर्वांगसमता नियम से,
ΔNOQ ≅ ΔPOM
अत: NQ = PM ...(i) (CPCT द्वारा)
और ∠QNO = ∠MPO (एकांतर कोण)
अत: NQ ॥ PM ...(ii)
समी० (i) तथा (ii) से,
NQPM एक समांतर चतुर्भुज है ।
अब QM विकर्ण वृत्त का व्यास है। (दिया है)
इसलिए, ∠N = 90° तथा ∠P = 90° है। (अर्धवृत्त में बना कोण 90° होता है)
अत: NQPM एक आयात है ।
(वह समांतर चतुर्भुज जिसका एक कोण समकोण हो वह आयत कहलाता है)
प्रश्न 8. यदि एक समलंब की असमांतर भुजाएँ बराबर हों, तो सिद्ध कीजिए कि वह चक्रीय है।
Solution
दिया है : ABCD एक समलंब है जिसमें
AB || CD है और AD = BC है |

सिद्ध करना है: ABCD एक चक्रीय चतुर्भुज है |
प्रमाण:
ΔACD तथा ΔBDC में,
AD = BC (दिया है)
DC = DC (दिया है)
∠DAC = ∠CBD (एक ही वृत्त खंड में बने कोण)
SAS सर्वांगसमता नियम से,
ΔACD ≅ ΔBDC
अत: ∠D = ∠C ...(i) (CPCT द्वारा)
अब चूँकि AB || CD दिया है इसलिए,
∠A + ∠D = 180° (अत: आसन्न कोणों का योग)
⇒ ∠A + ∠C = 180° [समी० (i)से]
अत: ABCD एक चक्रीय चतुर्भुज है |
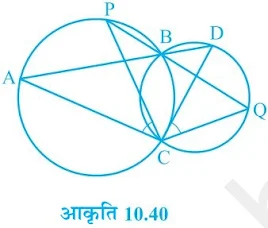
प्रश्न 9. दो वृत्त दो बिन्दुओं B और C पर प्रतिच्छेद करते हैं । B से जाने वाले दो रेखाखंड ABD और PBQ वृतों को A, D और P, Q पर क्रमश: प्रतिछेद करते हुए खींचे गए हैं (आकृति 10.40)। सिद्ध कीजिए कि ∠ACP = ∠QCD है |
Solution
दिया है: दो वृत्त दो बिन्दुओं B और C पर प्रतिच्छेद करते हैं। B से जाने वाले दो रेखाखण्ड ABD और PBQ वृत्तों को A, D और P, Q पर क्रमश: प्रतिच्छेद करते हुए खींचे गए हैं।
सिद्ध करना है: ∠ACP = ∠QCD
प्रमाण:
प्रथम वृत्त में, ∠ACP = ∠ABP (एक ही वृत्तखण्ड के कोण ) ...(i)
द्वितीय वृत्त में, ∠QCD = ∠QBD (एक ही वृत्तखण्ड के कोण ) ...(ii)
∠ABP = ∠QBD (शीर्षाभिमख कोण)
समी (i) तथा (ii) से,
∠ACP = ∠QCD
प्रश्न 10. यदि किसी त्रिभुज की दो भुजाओं को व्यास मानकर वृत्त खींचे जाएँ, तो सिद्ध कीजिए कि इन वृत्तों का प्रतिच्छेद बिन्दु तीसरी भुजा पर स्थित है।
Solution
दिया है: किसी AABC की दो भुजाओं AC तथा AB को व्यास मानकर दो वृत्त खींचे जाते हैं। दोनों वृत्त परस्पर एक-दूसरे को बिन्दु D पर प्रतिच्छेद करते हैं।
सिद्ध करना है: भुजा BC पर बिन्दु D स्थित है।
रचना: AD को मिलाइए।

प्रमाण:
चूँकि AC तथा AB दो वृत्तों के व्यास हैं।
∠ADB = 90° (चूँकि एक अर्द्धवृत्त का कोण है)
तथा, ∠ADC = 90° (चूँकि एक अर्द्धवृत्त का कोण है)
समी (i) तथा (ii) को जोड़ने पर,
∠ADB + ∠ADC = 90° + 90° = 180°
अत: BCD एक सरल रेखा है।
अतः D, भुजा BC पर स्थित है।
Solution
चूँकि उभयनिष्ठ कोण के साथ ∆ADC तथा ∆ABC दो समकोण त्रिभुज हैं।

भुजा AC को व्यास मानकर एक वृत्त खींचा जाता है जो बिन्दु B तथा D से होकर गुजरता है BD को मिलाते हैं।
∵ एक ही वृत्तखण्ड में कोण बराबर होते हैं।
∴ ∠CBD = ∠CAD
प्रश्न 12. सिद्ध कीजिए कि चक्रीय समान्तर चतुर्भुज आयत होता है।
Solution
दिया है: एक वृत्त के अन्तर्गत एक समान्तर चतुर्भुज PQRS है।
सिद्ध करना है: PQRS एक आयत है।

प्रमाण:
चूँकि PQRS एक चक्रीय चतुर्भुज है
∴ ∠P + ∠R = 180° ...(i)
(∵ एक चक्रीय चतुर्भुज में सम्मुख कोणों का योग 180° होता है)
परन्तु, ∠P = ∠R ...(ii)
(∵ समान्तर चतुर्भुज में सम्मुख कोण बराबर होते हैं)
समी (i) तथा (ii) से,
∠P = ∠R = 90°
इसी प्रकार,
∠Q = ∠S = 90°
∴ PQRS का प्रत्येक कोण 90° है।
अतः PQRS एक आयत है।